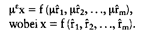Homogenität

numerische Massgrösse für den Verlauf einer (Produktions-)Funktion. Eine Funktion f heisst homogen vom Grad e, wenn gilt:

Eine vom Grad Eins homogene Funktion heisst linear homogen. Der Homogenitätsgrad ist identisch mit der (dann konstanten) Skalenelastizität.

Homogenität ist ein anderer Begriff für Gleichartigkeit. Gegensatz: Heterogenität.

1. Homogenität von Gütern: Fehlen von Präferenzen sachlicher, persönlicher, räumlicher und zeitlicher Art auf seiten der Käufer und Verkäufer auf einem Markt. Homogenität eines Gutes ist die Voraussetzung für das Vorliegen eines vollkommenen Marktes (-) Marktformen). Bestehen auf einem Markt Präferenzen nach einem oder mehreren dieser Kriterien, so sind die Güter inhomogen, und der Markt ist unvollkommen.
2. Homogenität von mathematischen Funktionen: Mathematisches Konzept von Bedeutung insbes. in der Produktions- und Nachfragetheorie. Eine Funktion y = y (x 1, xm) ist homogen, wenn eine Vermehrung aller unabhängigen Variablen auf das ?<,-fache eine Vermehrung der abhängigen Variablen auf das AA-fache herbeiführt: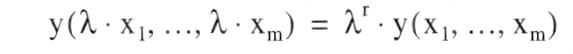

Die Konstante r heißt der Homogenitätsgrad. Sie gibt zugleich die – Elastizität der abhängigen Variablen bezüglich des Faktoreinsatzes bei simultaner Variation aller Einsatzmengen um gleiche Prozentsätze an. Im Spezialfall r = 1 heißt die Funktion linear-homogen. In der Produktionstheorie werden homogene Produktionsfunktionen oft benutzt. Ihr Homogenitätsgrad ist identisch mit der Skalenelastizität. Für r = 1 liegen constant returns to scale vor, bei r < 1 handelt es sich um decreasing returns to scale und bei r > 1 um increasing returns to scale. Kostenfunktionen, die auf dem Kostenminimierungsprinzip beruhen, sind homogen vom Grade 1 in den Faktorpreisen, d.h., proportionale Änderungen aller Faktor-preise verändern die Kosten einer vorgegebenen Produktionsmenge um denselben Prozentsatz. Nachfragefunktionen von Haushalten auf Grundlage des Nutzenmaximierungsprinzips sind homogen vom Grade 0 im Einkommen und den Güterpreisen, d.h., proportionale Änderungen dieser Größen verändern die Nachfrage nach jedem einzelnen Gut nicht. Literatur: Schumann, J. (1992). Hesse, H., Linde, R. (1976a)

Siehe homogene Konkurrenz, mikroökonomische Haushaltstheorie

Vorhergehender Fachbegriff: Homogenes Produkt | Nächster Fachbegriff: Homogenität

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Geldvolumen | Erwartungs-Valenz-Theorien | Vermögensstrukturkennzahlen

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer