Regression

Steuerregression

(Regressionsanalyse): Während es bei der Korrelationsanalyse um die Messung der Intensität des Zusammenhangs zwischen zwei oder mehreren Datenreihen geht, geht es bei der Regressionsanalyse um die Untersuchung der stochastischen Abhängigkeiten zwischen Variablen und der Möglichkeiten ihrer funktionalen Beschreibung durch statistische Analyse der funktionalen Abhängigkeit einer Zielvariablen (Kriteriumsvariablen) und einer oder mehreren erklärenden Variablen (Prädiktorvariablen).
Aufgabe der Regressionsanalyse ist es mithin, die genaue Struktur der die Datenreihen verknüpfenden Beziehung in Form einer Gleichung darzustellen. Die Regressionsanalyse stellt also den Versuch der Beantwortung zweier Aspekte des Zusammenhangs zwischen der abhängigen Zielvariablen und der oder den unabhängigen Prädiktorvariablen dar, nämlich erstens Frage nach der Art der Veränderung der Zielvariablen und zweitens nach der Größe der Veränderung. Das Prinzip aller Verfahren der Regressionsanalyse besteht in der möglichst genauen Anpassung einer theoretischen Funktion an die empirischen Wertepaare, wie sie in einem Streuungsdiagramm dargestellt werden können. Neben der Freihandmethode nach Augenmass, wird dazu in der Statistik meist die Methode der kleinsten Quadrate gewählt.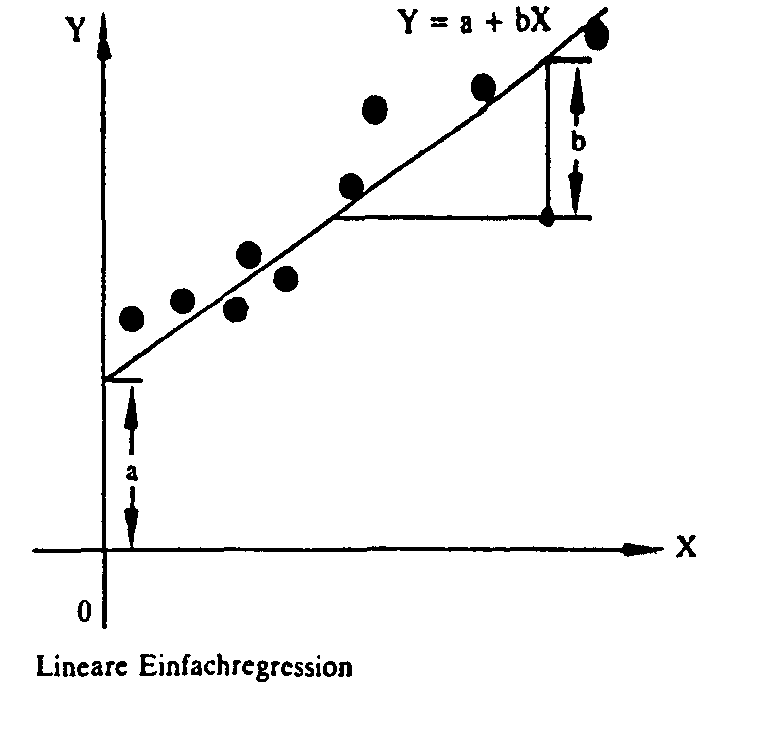

In der Regressionsrechnung ist zwischen vier Fällen zu unterscheiden:
1. der linearen Einfachregression,
2. der linearen Mehrfachregression,
3. der nichtlinearen Einfachregression und
4. der nichtlinearen Mehrfachregression:

1. Die lineare Einfachregression: Die allgemeine Gleichung für eine lineare Beziehung zwischen der erklärenden Variablen X und der Zielvariablen Y lautet: Y = a + bX die Formel für die Regressionsgerade. Darin ist a die Regressionskonstante und b der Regressionskoeffizient. Sie werden nach der Methode der kleinsten Quadrate so bestimmt, dass die Regressionsgerade den beobachteten Wertepaaren optimal angepaßt ist.

2. Die lineare Mehrfachregression: Die allgemeine Gleichung für eine lineare Beziehung zwischen mehreren erklärenden Variablen xi (i = 1, 2, ..., n) und einer Zielvariablen Y lautet: Y=a+biX1+b2x2+...b”Xn+e,.
Darin bezeichnet e1 eine additive Zufallsvariable. Auch in diesem Fall lassen sich die Werte a und b berechnen.

3. Die nichtlineare Einfachregression: sie hat die Gleichung Y = aXb.

4. Die nichtlineare Mehrfachregression: Ihre Gleichung lautet
V=a+b1X+b2x2.

Vorhergehender Fachbegriff: Regress | Nächster Fachbegriff: Regression, logistische

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Belegleser | Bank for International Settlements (BIS) | Beschäftigungsabweichung

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer