Optimierung

(1) In der Mathematik steht Optimierung für das Aufsuchen des größten oder kleinsten Wertes einer Funktion, bezeichnet also gleichermaßen Maximierung und Minimierung.

(2) Allgemein versteht man unter Optimierung die bestmögliche Lösung eines bestimmten Problems.

Hinweis:
Optimierungsverfahren bieten die Methoden des Operations Research und hier insbesondere die lineare Programmierung (LP).

ist die bestmögliche Lösung eines Problems unter Berücksichtigung aller relevanten Kriterien. Die hierfür erforderlichen Techniken zur Verfügung zu stellen ist Aufgabe des Operations Research. lineare Programmierung Optimierungsverfahren

(= mathematische Programmierung) stellt Verfahren zum Auffinden und Untersuchen einer Lösung folgender Problemstellungen zur Verfügung: Eine Funktion in einer oder mehreren Variablen (oder Funktionen) ist zu maximieren bzw. minimieren, wobei u.U. zusätzliche Restriktionen bezüglich dieser Variablen (oder Funktionen) zu beachten sind. Diese als Programmierungsprobleme bezeichneten Aufgabenstellungen sind im Bereich der Wirtschaftswissenschaften sehr häufig anzutreffen (z.B. gewinnoptimale - Allokation knapper Ressourcen), was das große Interesse an Optimierungsverfahren auf diesem Gebiet erklärt. Das allgemeine Programmierungsproblem lautet: Optimiere die Zielfunktion z = z unter Beachtung der m Restriktionen g,(x, ..... x) {5, = ,> } b;, 1 5 i G m, mit g;Lx): = bekannte Funktionen in den n Variablen xi (1 <_ j <_ n), b;: = gegebene Konstanten. a) Die einfachste davon erfaßte Aufgabenstellung ist die mit Hilfe der Differentialrechnung klassische Bestimmung der optimalen Werte x;* .... An* für den Fall m = 0; sind zusätzliche Restriktionen in Gleichungsform zu beachten (m > 0), ist ein Lösungsansatz die Multiplikatorregel von LAGRANGE. Die Anwendung der Differentialrechnung führt jedoch oft zu rechentechnischen Schwierigkeiten, so dass auf andere Verfahren zurückgegriffen werden muß. Sind Zielfunktion und die als Gleichungen oder Ungleichungen formulierten Restriktionen linear, also z(x) = cixj und g&(X) = E°_ a+jxi , (1 <_ i m), ca3: = Konstanten, liegt die Problemstellung der Linearen Programmierung vor, die unter Beachtung der Nichtnegativitätsforderungen an die xi z.B. mit Hilfe der Simplexmethode gelöst werden kann. Sind Zielfunktion und/oder Restriktionen nichtlineare Funktionen in den xi, ist die Aufgabenstellung der Nichtlinearen Programmierung gegeben, für die jedoch im Gegensatz zu linearen Problemen kein allgemeingültiges Lösungsverfahren existiert; es liegen nur Methoden für bestimmte Problemklassen vor. Das Lösen nichtlinearer Optimierungsaufgaben ist relativ schwierig. b) Eine weitere im allg. Programmierungsproblem enthaltene Aufgabenstellung ist gegeben, wenn es nicht um Parameteroptimierung, sondern um die Optimierung eines Funktionals geht, die xi also Funktionen in einem oder mehreren Parametern, z.B. der Zeit t, sind. Die einfachste Problemstellung dieser Art lautet: Man bestimme diejenige Funktion x = x(t) bzw. x\'(t), für die das Integral unter Beachtung von x(tA) =: A und x(tE) _: E optimiert wird. Optimierungsprobleme dieser Struktur heißen Variationsprobleme und können mit Hilfe der von Leonhard EULER und Joseph de LAGRANGE entwickelten Variationsrechnung gelöst werden; die notwendige Bedingung für das Vorliegen eines Optimums gibt dabei das EULERsche System gewöhnlicher Differentialgleichungen oder die HAMILTON-JACOBIsche partielle Differentialgleichung an. c) Sind nun mehrere Funktionen der unabhängigen Variablen gegeben und führt man die zusätzlichen Restriktionen ein, dass einige dieser Funktionen gewöhnlichen Differentialgleichungen folgen, bezeichnet man diese Funktionen als Lagekoordinaten xi(t) und die freien Funktionen als Steuerfunktionen uk(t), so kommt man zu einer weiteren im allg. Programmierungsproblem enthaltenen Klasse von Optimierungsaufgaben: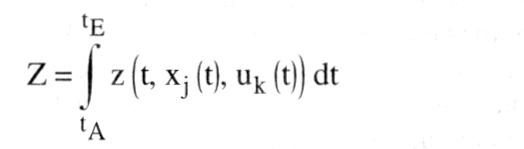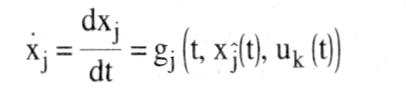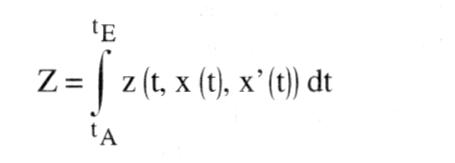

Man bestimme diejenigen Steuerfunktionen uk(t), für die die Zielgröße unter Beachtung der Restriktionen und der Randwertbedingungen xi(tA) A.xi(tE) Ei(1 < j, 1 < m; I < k < 1) optimiert wird. Fragestellungen dieser Art sind Grundprobleme der - Kontrolltheorie, die über eine geeignete Festlegung der Zeitpfade für die Steuerfunktionen (= Kontrollvariablen) ein Optimum der Zielfunktion erreichen möchte. Derartige dynamische Optimierungsprobleme sind im ökonomischen Bereich zahlreich gegeben. Die Lösung dieser Klasse von Optimierungsproblemen, die auch z.B. als diskrete Aufgabenstellungen gegeben sein können, ist mit Hilfe des PONTRYAGINschen Maximumprinzips, des Gradientenverfahrens, des Verfahrens der Dynamischen Programmierung nach Richard BELL-MAN, aber auch mit Hilfe einer Weiterentwicklung der klassischen Variationsrechnung möglich. Literatur: Föllinger, O. (1985). Tolle, H. (1971). Frank, W. (1969)

Vorhergehender Fachbegriff: Optimierende Entscheidungsregel | Nächster Fachbegriff: Optimierung, dynamische

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Wirtschaftsberatung | Grenzplankostenrechnung | Bezugsgrößenkombination

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer