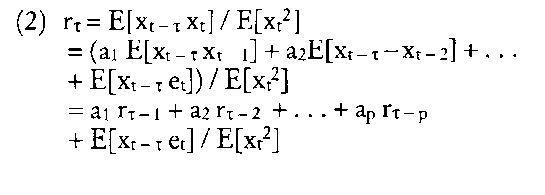Box-Jenkins-Verfahren

wichtigste und in der Praxis weit verbreitete Variante der autoregressiven Verfahren, die zur Absatzprognose nur die tatsächlichen Absatzwerte der Vergangenheit heranziehen. Jeder Zeitreihenwert ist als Summe dermit Parametern (ai) gewogenen vergangenen Zeitreihenwerte plus einer Störvariablen et darstellbar:
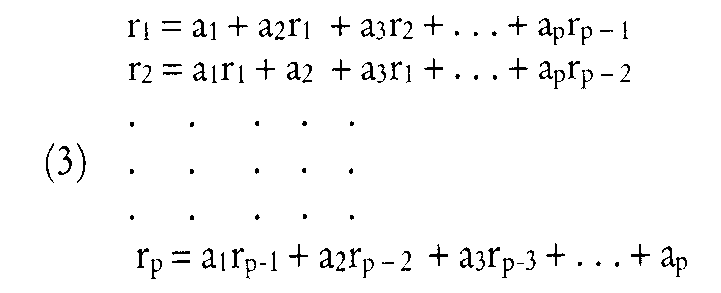Box-Jenkins-Verfahren

Diese Gleichung heißt autoregressiver Prozeß p-ter Ordnung (AR(p)-Prozeß). Die Parameter ai sind so zu schätzen, dass der Wert xt möglichst gut angenähert wird. Dazu benutzen Box und Jenkins die Autokorrelationsfunktion rx (t= 1,2. . .), wobei X den zeitlichen Abstand (time lag) bedeutet:
Box-Jenkins-Verfahren

Da die Störvariable ct mit den Zeitreihenwerten nicht korreliert ist, verschwindet der letzte Summand. Läßt man nun X von 1 bis p laufen, erhält man ein lineares Gleichungssystem mit p Gleichungen, die sog. Yule-Wal- ker-Gleichungen (wobei zu beachten ist, dass r0 = 1 undr-i = n). Wegen der Symmetrie des timelags gilt:
Box-Jenkins-Verfahren

Liegt ein AR(p)-Prozeß vor, so sind alle Parameter ai bis i = p ungleich Null, danach gleich Null. Man kann also die Ordnung p des Prozesses bestimmen, indem man für p dicWertel,2,.. .einsetzt und das resultierende Gleichungssystem so oft löst, bis ap gleich Null wird. Ein zweiter Weg, Zeitreihen zu prognostizieren, besteht darin, den Zeitreihenwert xt durch die Vergangenheitswerte der Störvariablen et auszudrücken: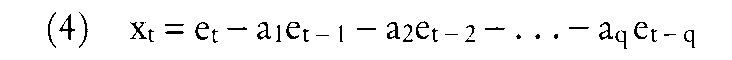
Box-Jenkins-Verfahren

Diese Gleichung heißt Moving-Average- Prozeß q-ter Ordung (MA(q)-Prozeß). Auch hier können die Parameter a; und die Ordnung q in ähnlicher Weise ermittelt werden wie beim AR(p)-Prozeß. Allerdings ist hier ein nicht-lineares Gleichungssystem zu lösen, was nur auf iterativem Wege oder durch eine Taylor-Entwicklung möglich ist. Faßt man AR(p)- und MA(q)-Prozesse zusammen, so entsteht ein ARMA(p,q)-Prozeß, der sich der Struktur einer Zeitreihe noch besser anpaßt. Mit ARMA-Modellen lassen sich jedoch nur stationäre Zeitreihen prognostizieren. Enthält eine Zeitreihe einen linearen Trend, so kann sie durch Differenzenbildung in eine stationäre Reihe umgeformtwerden. Trend-Reihe: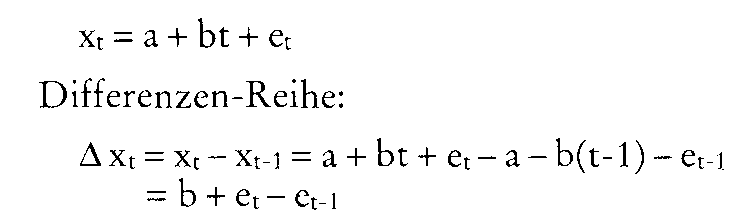

Auf diese stationäre Reihe kann nun das Box-Jenkins-Verfahren angewendet werden. Anschließend muss die Differenzen- Reihe wieder „integriert“ werden, um zur ursprünglichen Reihe zurückzukehren. Box und Jenkins haben diesen allgemeinen Prozeß „Autoregressive integrated moving average“ (ARIM A) genannt, um anzudeuten, dass auch nichtstationäre Zeitreihen prognostiziert werden können.

Literatur: Box, G. E. P.; Jenkins, G. M., Time Series Analysis, San Francisco 1976.

Vorhergehender Fachbegriff: Box-Jenkins-Modelle | Nächster Fachbegriff: Boxdiagramm

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Handlungsrechte | Gewinnspiele,Preisausschreiben | Relationenmodell

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer