dynamische Optimierung

Bei der Dynamischen Optimierung (DO) werden Optimierungsmodelle betrachtet, die so in einzelne Stufen (z.B. Zeitabschnitte) zerlegt werden können, dass die Gesamtoptimierung durch eine stufenweise, rekursive Optimierung ersetzbar ist. Anwendungen findet man u.a. bei der Bestellmengen- und Losgrößenplanung. Lösungsverfahren für Modelle der DO basieren auf dem Bellman’schen Optimalitätsprinzip.

Typ von Entscheidungsbaumverfahren der kombinatorischen Optimierung, zur Klasse der impliziten vollständigen Enumeration gehörend. Sie wurde von Richard E. Bellman in den 50er Jahren entwickelt und auf zahlreiche kombinatorische Optimierungsprobleme angewandt. Sowohl in der Organisation des Baumes als auch in der Terminologie unterscheidet sich die dynamische Optimierung von den prinzipiell verwandten Verfahren des Branch and Bound und der begrenzten Enumeration. Bei der dynamischen Optimierung werden die Enumerationsbäume parallel, in Stufen, aufgebaut. Zu jeder "Stufe" werden sämtliche "Zustände" berechnet. Unter "inhaltlich identischen" Zuständen werden die unterlegenen Zustände gestrichen. Als Beispiel sei ein Verkehrsnetz mit den Orten A bis D betrachtet, zwischen denen direkte Strassenverbindungen mit den folgenden Längen (in km) bestehen. 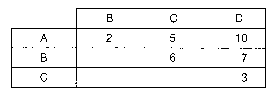dynamische Optimierung

Gefragt sei nach den kürzesten Strassenfolgen vom Ort A aus zu allen anderen Orten. Mit Hilfe der dynamischen Optimierung würde man von A zunächst alternativ zu B, C und D mit den Entfernungen 2, 5 bzw. 10 gehen (vgl. Entscheidungsbaum). Sodann würde man nach einem von E. W. Dijkstra vorgeschlagenen Verfahren von dem Ort weitergehen, der die jeweils kürzeste Entfernung vom Ausgangsort hat, hier also von B aus, gelangt dabei auf die Stufe 2, kann die direkten Wege mit den Wegen über B (als "inhaltlich identisch") vergleichen und den jeweils schlechteren Weg streichen. In der Stufe 3 würde man den nächstnahen Ort C auswählen, etc. Man erhält für den Weg von A nach D mit anfangs 10 km auf der Stufe 2 den verbesserten Weg über B mit 9 km und auf der Stufe 3 den weiter verbesserten Weg über C mit 8 km.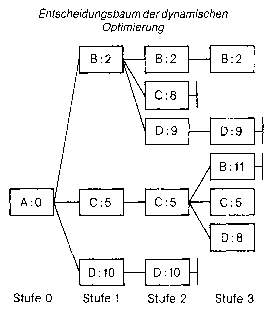

Das für die dynamische Optimierung charakteristische Vergleichen von inhaltlich identischen Zuständen derselben Stufe ist dem Bewerten von Teillösungen der begrenzten Enumeration bzw. von Lösungsmengen des Branch and Bound teilweise überlegen, teilweise deutlich unterlegen, je nach Problemtyp. Doch sind Kombinationen von beiden Prinzipien möglich. Literatur: Bellntann, R. E., Dynamic Programming, Princeton, N.J. 1957. Dijkstra, E. W., A Note on Two Problems in Connection with Graphs, in: Numerische Mathematik, 1. Jg., S. 269 ff. Hu, T.C., Combinatorial Algorithms, Reading, Mass. 1982.

Gebiet der mathematischen Optimierung, das sich mit der Lösung von Problemen der optimalen Steuerung mehrstufiger wirtschaftlicher oder technischer (Entscheidungs-)Prozesse im Zeitablauf befaßt. Der Zustand des betrachteten Systems wird in jedem Zeitpunkt eines bestimmten Zeitintervalls (= Planungszeitraum) RA; tEj durch den Zustandsvektor x der Zustandsvariablen xt, ..., xm beschrieben; das zeitliche Verhalten des Systems ist durch die Wahl der in Folge getroffenen Entscheidungen, ausgedrückt durch den Vektor der Entscheidungsvariablen (= Steuervariablen, Kontrollvariablen) u = (u\', ..., u&) bestimmt. Der Planungshorizont kann endlich oder unendlich sein. Gesucht ist die optimale Politik (Steuerung), also eine Folge von Entscheidungen, die eine den Prozess bewertende Zielgröße optimiert. Die dynamische Optimierung entspricht somit dem unter - Kontrolltheorie bekannten Gebiet. Dynamische Optimierungsprobleme sind innerhalb der Wirtschaftswissenschaften sehr häufig gegeben ( ökonomische Modelle mit exogenen, endogenen und Instrumentvariablen, Zuordnungs- oder Lagerhaltungsprobleme, Probleme der - Spieltheorie); eine mathematsiche Standardformulierung des dynamischen Optimierungsproblems existiert (im Gegensatz zu linearen Programmierungsproblemen) nicht. Grundsätzlich können diskrete und stetige Aufgabenstellungen unterschieden werden. a) Ein diskretes, deterministisches, endliches dynamisches Optimierungsproblem kann folgendermaßen beschrieben werden: Der Entscheidungsprozess ist in endlich viele Stufen j zerlegbar, das Intervall [tA; tE] also in endlich viele Teilintervalle eingeteilt; jeder Stufe ist eine bestimmte Anzahl von Zuständen zugeordnet, und auf jeder Stufe ist eine Strategieentscheidung zu treffen, die bewirkt, dass der momentane Zustand xi in einen der nächsten Stufe zugeordneten Zustand xi+4 übergeht. Eine Änderung erfolgt also nur von Stufe zu Stufe, nicht innerhalb eines Teilintervalls. Unter Berücksichtigung der Menge der Zustände (= Zustandsraum Xi), der Entscheidungen (= Entscheidungsraum Ui) und der möglichen Transformationen gj (gi e G,) pro Stufe soll das Optimum einer gegebenen Zielfunktion erreicht werden, wobei ein Zustand einer Stufe eindeutig durch einen bestimmten Zustand der Vorstufe und der auf der betrachteten Stufe zu treffenden Entscheidung bestimmt wird, also: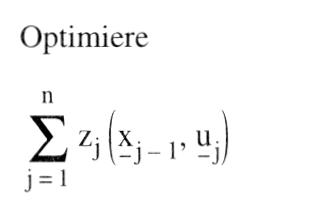
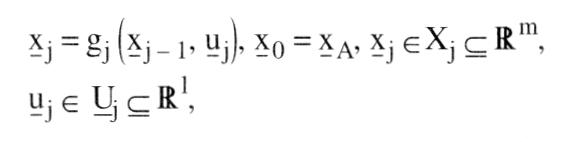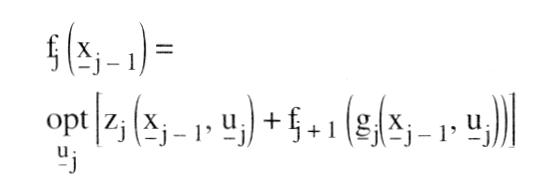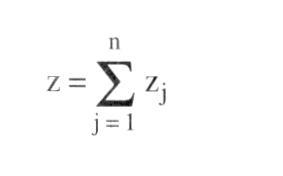dynamische Optimierung

unter den Nebenbedingungen
dynamische Optimierung

die dynamische Nebenbedingung für rxj stellt dabei eine Differenzengleichung dar. Die Lösung dieses Problems ist mit Hilfe der BELLMANschen Funktionalgleichungsmethode möglich, wobei der mehrstufige Optimierungsprozess in eine Rekursionsbeziehung transformiert wird, deren Lösung leichter zu finden ist. Sie beruht auf dem BELLMANschen Optimalitätsprinzip, das besagt, dass auf der Stufe j (1 <_ j <_ n) eines n-stufigen Prozesses eine optimale Politik (s......) für den Restprozess existiert, die nur von dem Zustand xi_, der Vorstufe und nicht von den vorangegangenen Entscheidungen ui,...,u~ abhängig ist. Die sich aus diesem Prinzip ergebende Rekursionsbeziehung lautet für festes j mit ff+1 E
0. Das Lösungsverfahren beginnt mit der Suche der optimalen Entscheidung auf der letzten Stufe und bestimmt mit Hilfe obiger Beziehung sukzessive die optimale Politik aller vorangegangenen Stufen. Dieses Verfahren ist auf Probleme mit unendlichem Planungshorizont (n –a oo) übertragbar. Ein anderes Lösungsverfahren ist die Gradientenmethode; Verfahren auf der Grundlage des PONTRYAGINschen Maximumprinzips spielen in der diskreten dynamischen Optimierung kaum eine Rolle. Ist ein Zustand xj nicht eindeutig durch den Zustand xi_i und der zu treffenden Entscheidung ui bestimmt, sondern als Zufallsgröße aufzufassen, deren bedingte Eintrittswahrscheinlichkeit zusätzlich von der bis zur Stufe j realisierten Vorgeschichte abhängt, liegt ein stochastisches Optimierungsproblem vor, für welches nur Wahrscheinlichkeitsaussagen über den Prozeß-verlauf möglich sind. Ist in einem stochastischen System speziell xi nur von xi.l abhängig, kann also vi_i durch x~ ersetzt werden, und sind die Übergangswahrscheinlichkeiten von einem Systemzustand zum nächsten bekannt, so kann der Prozess als MARKOV-Prozess beschrieben werden; Stufen können dabei unendlich oft wiederkehren. Der für die deterministische dynamische Optimierung beschriebene Lösungsweg ist übertragbar. b) Läßt sich der Planungszeitraum [tA; tE] nicht mehr derart in Stufen einteilen, dass der Systemzustand sich nur von Stufe zu Stufe ändert, innerhalb eines Teilintervalls jedoch alle das Systemverhalten bestimmenden Größen konstant sind, liegt die Aufgabenstellung der stetigen deterministischen dynamischen Optimierung vor, deren Standardproblem lautet: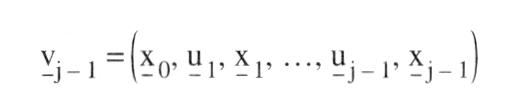
dynamische Optimierung

x wird dabei auch als »Trajektorie«, X(tE) als Zielmenge bezeichnet; die Steuervariablen u1, ..., u\' sind aus der Klasse der auf [tA; tE] LEBESGUE-integrierbaren Funktionen zu wählen. Die dynamische Nebenbedingung stellt jetzt eine Differentialgleichung dar; die zeitliche Änderung des Systemzustandes hängt nun auch explizit vom Zeitpunkt t ab. Sind alle Funktionen g für alle t e [tA; tE] linear, spricht man von linearen Kontrollproblemen. Liegen Beschränkungen für die Steuervariablen vor, tritt das Problem möglicher Randlösungen auf. Die Lösung dieses Optimierungsproblems ist mit Hilfe der BELLMANschen Funktionalgleichungsmethode für stetige Aufgabenstellungen, der Variationsrechnung, des Gradientenverfahrens oder auf der Grundlage des Maximumprinzips von PONTRYAGIN unter Benutzung der HAMILTON-Funktion möglich. Bei nichtlinearen Problemen kann das Maximumprinzip nur in speziellen Fällen genutzt werden; dann ist die Anwendung von Gradientenverfahren erforderlich, die die Lösung allgemeiner Optimierungsprobleme in normierten Räumen ermöglichen. Läßt man zu, dass mehrere Instanzen den Entscheidungsprozess über die Wahl der Steuervariablen beeinflussen können, kommt man zu Problemen der Spieltheorie, die entsprechend zu lösen sind. Literatur: Chiang, C.A. (1992). Seierstad, A., Sydsaeter, V. (1987). Neumann, K. (1977). Hadley, G. (1969). Bellman, R. (1957)

Vorhergehender Fachbegriff: Dynamische Nutzenbalance | Nächster Fachbegriff: dynamische Produktionsfunktionen

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Residualeinkommen | Hochschule | Ringi Seido

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer