| Empfehlungen |  |
Informationswert
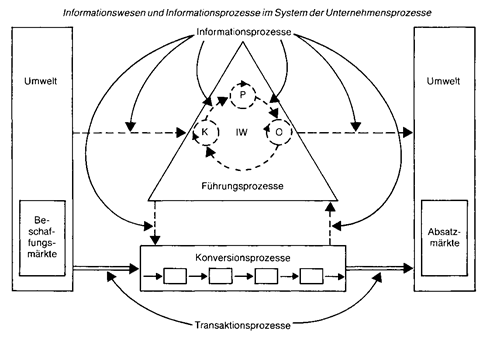 In der betriebswirtschaftlichen Entscheidungstheorie gibt es verschiedene Versuche einer näherungsweisen quantitativen Ermittlung des Infor mations wer tes. Grundlage sind zumeist Erwartungswerte bei Entscheidungen, wobei man einmal vom Fehlen und das andere Mal von der Verfügbarkeit zusätzlicher Information ausgeht. Der Bruttowert einer Information ergibt sich dann als Differenz der beiden Erwartungswerte. Die Beschaffung von Zusatzinformationen zur Verbesserung des Informationsstandes ist wirtschaftlich nur dann sinnvoll, wenn der Bruttowert grösser als die anfallenden Informationskosten ist. Der Nettowert, d.h. der um die Informationskosten verminderte Bruttowert der Information, muss also positiv sein. Da die Informationsbeschaffung im Rahmen der Marktforschung Kosten verursacht, wird sie selbst zum Entscheidungsproblem: Es muss entschieden werden, wie lange bzw. in welchem Umfange Informationen einzu- holen sind. Grundsätzlich scheint dies einfach: Nach dem marginalanalytischen Prinzip ist der Informationsbeschaffungsprozeß solange fortzusetzen, bis die Kosten der zusätzlichen Information gleich ihrem Nutzen („Wert“) werden. Damit rückt das Problem des Informationswertes in den Vordergrund. Die Lösung dieses Problems ist am weitesten durchgearbeitet im Bay es’\'sehen Ansatz („ BayesianApproach “): Der englische Geistliche Bayes entwickelte in seiner 1763 erschienenen Schrift „An Essay toward Sol- ving a Problem in the Doctrine of Chance“ eine Formel (Bayes’sches Theorem), die es ermöglicht, aus den bedingten Wahrscheinlichkeiten eines Ereignisses (Wahrscheinlichkeit für ein Ereignis - A unter der Bedingung, dass ein anderes - B - bereits eingetreten ist) quasi umgekehrt auf die Wahrscheinlichkeit des Ereignisses zu schließen, dessen Eintreten die Bedingung darstellt, nämlich die von B (unter der Bedingung, dass A eingetreten ist). Die Nutzung des „Bayes’schen Theorems“ für das vorliegende Problem erfolgt in drei Schritten: 1. Zunächst wird eine a-priori-Analyse durchgeführt. Dazu gehört: - Definition der verfügbaren (Handlungs-) Alternativen ai. - Definition der möglichen Umweltzustände Sj. - Durch die Bewertung (mit Ein- und Auszahlungen oder Opportunitätskosten - „entgangener Gewinn“) ergibt sich eine Entscheidungsmatrix. - Den einzelnen Umweltzuständen werden - i.d.R. subjektive - Wahrscheinlichkeiten zugeordnet; das Ergebnis ist ein „Erwartungswert“ für jede Alternative; die mit dem höchsten (bei der Zahlungs-Matrix) wird präferiert. Als Entscheidungsregel dient also „Maximierung des Erwartungswertes“. Beispiel: Der Einfachheit halber seien nur 2 Alternativen betrachtet: Einführung eines neuen Produkts (ai), Beibehaltung des alten (m). Der Umweltzustand si ist dadurch charakterisiert, dass mit einer „günstigen“ Entwicklung des Marktanteils gerechnet wird, bei S2 dagegen mit einer „ungünstigen“. Die Zahlungsmatrix sei wie folgt geschätzt (in Klammern die a-priori-Wanrscheinlich- keiten): 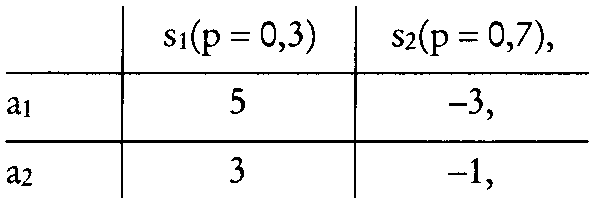 Damit ergeben sich folgende Erwartungswerte: ai: (5 • 0,3) + (3 • 0,7) = -0,6 a2: (3 ■ 0,3) + (1 ■ 0,7) = 0,2 Somit wäre Alternative 2, also die Beibehaltung des alten Produkts - oder, anders ausgedrückt: der V erzieht auf die Einführung eines neuen -, zu bevorzugen. 2. Die a-priori-Analyse wird ergänzt durch eine a-posteriori-Analyse. Das bedeutet, dass nunmehr die bedingten Wahrscheinlichkeiten herangezogen werden. Dieser Schritt dient der „Verbesserung“ der a- priori-Wahrscheinlichkeiten und sollte im Grunde mittels empirischer Daten (statt bloßer Schätzungen) erfolgen. Im Beispiel soll so vorgegangen werden, dass die Ein- und Auszahlungen für die Alternative „Beibehaltung des alten Produkts" gleich 0 gesetzt werden und die Daten für die Alternative 1 (Produkteinführung) quasi nur die Differenzen zu Alternative 2 darstellen. Insofern gelten auch die Wahrscheinlichkeiten nur für die Alternative „Produkteinführung“ und können - da diese nur „Annahme“ oder „Ablehnung“ (des neues Produkts) heißt - mittels der Binominalverteilung, aufgrund einer empirischen Befragung, berechnet werden. Angenommen, diese erbringe, dass 8 von 10 insgesamt Befragten ai präferie- ren. Aus der Formel für die Binominalverteilung ergibt sich dann als bedingte („conditio- nal“) Wahrscheinlichkeit für si 0,121 und S2 0, 0106. Multipliziert man dies mit den ursprünglichen Wahrscheinlichkeiten, so resultiert die »joint probability“. Dividiert man jede einzelne davon durch ihre Summe, so erhält man - entsprechend dem „Bay- es’schen Theorem“ - schließlich die a-poste- riori-Verteilung:  Der Erwartungswert ist nunmehr ein anderer. Stellt man nur auf die Alternative 1 ab, setzt also die Ein- und Auszahlung für a2 gleich 0 (was angesichts dessen, dass als Indikator für die „wahren“ Umweltzustände nur die „Adaption“ des neuen Produktes verwandt wurde, plausibel erscheint), so ergibt sich: (5 -0,83) + (3 -0,17) = 3,64. Im Vergleich zu 0 wäre also jetzt die Alternative 1 vorzuziehen. Dasselbe Resultat folgt allerdings auch dann, wenn man die Art der eingeholten Information als adäquates Indiz für die „wahren“ Umweltzustände in bezug auf beide möglichen Handlungsalternativen ansieht und demgemäß auf die oben wiedergegebene Zahlungsmatrix abstellt. Das ergibt: für ai 3,64, gem. oben für a2 (3 ■ 0,83)+ (1 • 0,17) = 2,32 2. Daraus resultiert auch die Möglichkeit, den Wert zusätzlicher Informationen abzuschätzen, mittels der prae-posteriori- Analyse. Hierzu ist zunächst der “erwartete Wert vollkommener Information“ („Expected Value of perfect Information “ = EVI) zu berechnen. Er bezeichnet die Größe, die aus der Differenz des Wertes resultiert, der sich ergibt, wenn der Entscheidende weiß, welche Reaktionen auf seine Maßnahmen eintreten, und dem Auszahlungserwartungswert der optimalen Entscheidung bei unvollkommener Information. Im Beispiel folgt: EVI = [(5 • 0,3) + ( 1 • 0,7)] [(3 • 0,3) + ( 1 ■ 0,7)] = 0,8-0,2 = 0,6 Der EVI-Wert stellt also quasi die „Kosten der Ungewißheit“ dar. Damit bildet er zugleich die Obergrenze für die Kosten zusätzlicher Informationen. Die Frage lautet also, ob tatsächlich zusätzliche Informationen eingeholt werden sollen, um eine a-posterio- ri-Analyse durchführen und damit möglicherweise die Entscheidung verbessern zu können. Dies eben ist Aufgabe der prae-po- steriori-Analyse; sie ist also, wie auch schon die Bezeichnung andeutet, vor der Beschaffung weiterer Informationen vorzunehmen. Das Problem dabei liegt darin, dass man gerade nicht weiß, wie die zusätzlichen Informationen lauten werden. Folglich muss für jeden Fall - bei festgelegtem Stichprobenumfang - eine besondere Analyse durchgeführt werden; daraus ist ein Gesamt-Resultat abzuleiten. Im obigen Beispiel von n = 10 wäre also die Berechnung jeweils vorzunehmen für x vonO, 1,..., 10.Derjeweilsoptimale(Erwar- tungs-)Wert müßte sodann, in der üblichen Weise, mit der dazugehörigen Wahrscheinlichkeit multipliziert und darüber summiert werden. Das Ergebnis dieser Berechnungen ist der “erwartete Wert der Stichprobeninformation “ („ Expected value of Sample Information “ = ESI). Subtrahiert man davon die Kosten der Stichprobe, so erhält man den “erwarteten Nettogewinn der Stichprobe“ („ Expected Net Garn of the Sample“ = ENGS); ist dieser größer als 0,so lohnt sich die zusätzliche Beschaffung von Informationen. Allerdings war hierbei ausdrücklich von einem festgelegten Stichprobenumfang ausgegangen worden. Gerade aber die erforderliche Größe der Stichprobe zur Gewinnung weiterer Informationen ist ebenfalls zu bestimmen. Damit ist im Grunde die prae-po- steriori-Analyse für verschiedene Stichprobenumfänge (mit der Beschränkung lediglich der Obergrenze der Kosten durch den EVI- Wert!) durchzuführen. Zugleich ist damit eines der vielen Probleme der - als rein formales Kalkül zweifellos bestechenden - Bayes-Analyse angesprochen. Damit im Zusammenhang steht, dass die Alternativen und vor allem auch die Umweltzustände gewissermaßen „diskretisiert“, auf einige wenige reduziert werden. Noch allgemeiner: Während die „klassische Statistik“ quasi nur eine bestimmte Hypothese testet, müssen bei der Bayes-Statistik sämtliche Alternativen und Umweltzustände nicht nur expliziert, sondern zusätzlich auch noch - mit Ein- und Auszahlungen - bewertet werden. Der Informationsbedarf ist also beträchtlich. Schätzungen sind v. a. auch für die a-priori- Wahrscheinlichkeiten notwendig. Rein subjektive Wahrscheinlichkeitsaussagen sind aber an die Person des Analytikers gebunden und nicht intersubjektiv nachvollziehbar. Ähnliche Probleme können auch bei der a- posteriori-Analyse entstehen: Wie schon das Beispiel zeigte, ist es oft nicht leicht, die den bedingten Wahrscheinlichkeiten zugrunde zu legenden Daten, als „Signal“ für den wahren Umweltzustand, hinreichend exakt zu bestimmen. Es bleibt schließlich durchaus offen, ob das der Bayes’schen Analyse inhärente Konzept des „Informationswertes“ nicht zu eng ist: Informationen vermögen auch anderen Zwecken als bloß Entscheidungen zu dienen. Sie können darüber hinaus auch Anlaß für das Erkennen neuer Umweltzustände und/oder Alternativen sein (und damit über die „Revision“ von Wahrscheinlichkeiten hinausgehen). Schließlich ist fraglich, ob die „ Maximierung des Erwartungswertes“ überhaupt bzw. durchweg eine sinnvolle Entscheidungsregel darstellt. Insgesamt bedeutet dies wohl, dass noch manche Hürde zu überwinden sem dürfte - wozu auch die Verbreitung entsprechender Computerprogramme und von etwaigen Anwendungserfahrungen gehört ehe in nennenswertem Umfange der praktische Einsatz erfolgen kann. Literatur: Hüttner, M., Informationen für Marketing-Entscheidungen, München 1979, S. 13 ff. Vorhergehender Fachbegriff: Informationsversorgung, Grundprinzipien | Nächster Fachbegriff: Informationswesen Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken |
|
Schreiben Sie sich in unseren kostenlosen Newsletter ein
Bleiben Sie auf dem Laufenden über Neuigkeiten und Aktualisierungen bei unserem Wirtschaftslexikon, indem Sie unseren monatlichen Newsletter empfangen. Garantiert keine Werbung. Jederzeit mit einem Klick abbestellbar.
Weitere Begriffe : Kanban-Steuerung | Integrationsthese | BSH
|
Praxisnahe Definitionen Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar. |
Fachbegriffe der Volkswirtschaft Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre. |
Beliebte Artikel Bestimmte Erklärungen und Begriffsdefinitionen erfreuen sich bei unseren Lesern ganz besonderer Beliebtheit. Diese werden mehrmals pro Jahr aktualisiert. |
