Katastrophentheorie

Ende der 60er Jahre von dem französischen Mathematiker René Thom begründete Theorie; "Katastrophen" können (nur) in nichtlinearen Systemen auftreten, und zwar durch abrupte Veränderungen der dynamischen Eigenschaften bei kleinen Parametervariationen. E. C. Zeeman verwendet ein Katastrophenmodell, um die Instabilitäten von Aktienmärkten zu untersuchen. Dabei werden zwei Anlegergruppen unterschieden; die Fundamentalisten treffen ihre Entscheidungen über Finanzinvestitionen aufgrund von Fundamentalanalysen. Die Chartisten richten dagegen ihre Anlageentscheidungen allein auf die vergangene Entwicklung der Aktienmärkte aus ( Chartanalyse). Spekulanten sind Anleger, die Risiken eingehen, um kurzfristige Preisdifferenzen gewinnbringend zu nutzen; sie sind mehrheitlich den Chartisten zuzuordnen. Die Dynamik der Aktienmärkte wird im Modell von Zeeman durch sieben Hypothesen über das Verhalten der Fundamentalisten und Chartisten beschrieben. Die Bewegungen auf dem Aktienmarkt erfolgen abwechslungsweise in Hausse- und Baissephasen, wobei der Übergang von einer Hausse in eine Baisse unter "normalen" Bedingungen, d. h. bei mässiger Spekulation, zu einer stetigen Aktien- indexsenkung führt. Eine Katastrophensituation ( Börsenkrach) kann nur dann eintre- ten, wenn der Anteil der Spekulanten am Gesamtwert des Aktienmarktes in der Hausse sehr stark zunimmt. Dann führt die Bewegung in die Katastrophenregion, so dass sich die dynamischen Eigenschaften der Aktienmärkte abrupt ändern, wodurch ein Aktienpreissturz erfolgt. Literatur: Ursprung, H. W., Die elementare Katastrophentheorie. Eine Darstellung aus der Sicht der Ökonomie, Berlin u. a. 1982. Zeeman, E. C., On the Unstable Behaviour of Stock Exchanges, in: Journal of Mathematical Economics, 1974, S. 39 ff.

mathematischer Ansatz zur endogenen Erfassung plötzlicher Sprünge einer oder mehrerer Variablen in dynamischen Systemen. Es sei ein zeit-stetiges dynamisches System der allgemeinen Form dx1/dt = f1 (x1,x2,x3) dx2/dt = f2 (x1,x2,x3) dx3/dt = f3 (x1,x2,x3) gegeben, wobei die Gleichungen die Veränderungen der Variablen im Zeitpunkt t in Abhängigkeit von dem augenblicklichen Wert aller Variablen angeben. In einem ersten Schritt werden die Variablen eines Systems in langsame und schnelle Variablen unterschieden. Im Extremfall verändert sich z.B. die Variable x1 unendlich viel schneller als die langsamen Variablen x2 und x3 für gegebene Zustandswerte aller drei Variablen. Bei dieser Annahme können die langsamen Variablen als Parameter interpretiert werden. In einem zweiten Schritt wird angenommen, dass die schnelle Variable x1 sich unendlich schnell ihrem Gleichgewichtswert (Analyse) anpaßt: Sind die langsamen Variablen (Parameter) gegeben und hat die Variable x1 aus irgendeinem Grunde einen anderen als ihren Wert im - Gleichgewicht angenommen, dann bewegt sich x1 unmittelbar auf diesen zu. Er sei durch x,* = g (x2,x3) beschrieben, um anzudeuten, dass dieser partielle Gleichgewichtswert von den Werten der langsamen Variablen abhängt. Wird die Funktion g geometrisch dargestellt, erhält man eine zweidimensionale Fläche M in einem x1-x2-x3-Diagramm: Bei gegebenen Werten der langsamen Variablen wird der gleichgewichtige x1-Wert stets als der zugeordnete Punkt »auf« der Fläche M abgelesen. Die von Rene THOM entwickelte »elementare Katastrophentheorie« versucht, solche Funktionen g zu finden, die bei einer kleinen Änderung der Funktion nicht zu einer essentiell anderen geometrischen Form der Gleichgewichtsfläche M führen (sog. strukturell stabile Funktionen).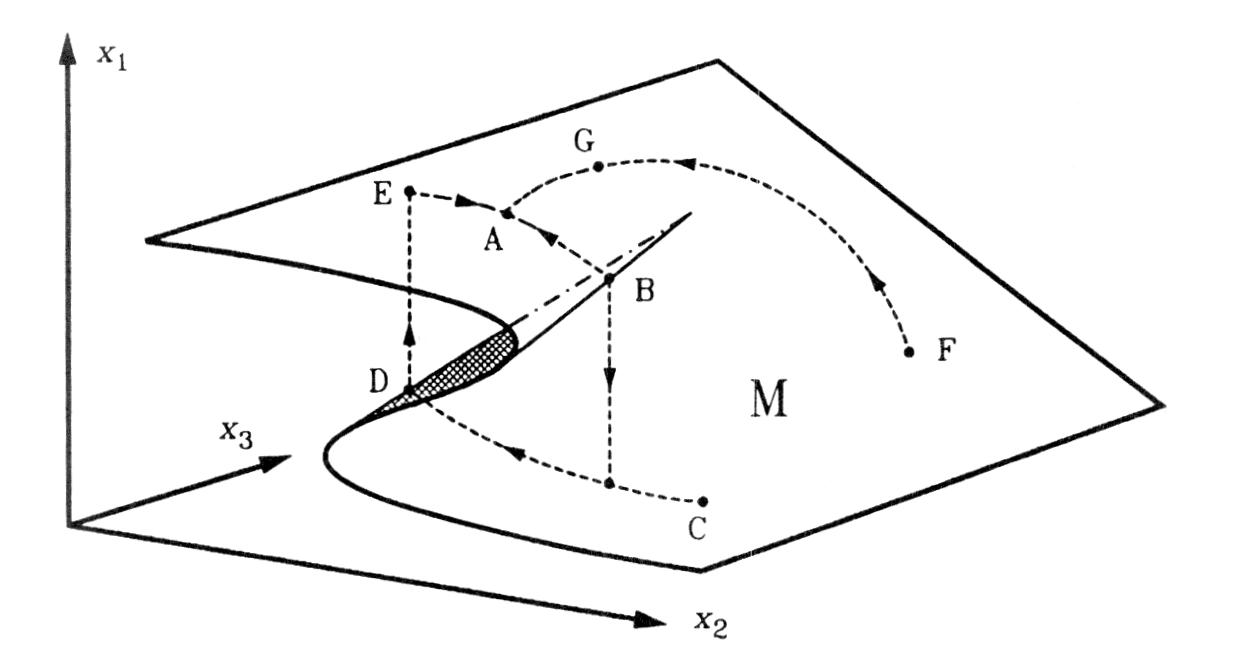

Bei Betrachtung einer einzigen schnellen Variablen sind dies vier verschiedene Funktionen; wird eine zweite schnelle Variable definiert, erhöht sich die Zahl der strukturell stabilen Funktionen um drei Formen. Von diesen sieben sog. elementaren Katastrophen enthalten fünf mehr als drei schnelle und/oder langsame Variablen, so dass eine vollständige geometrische Darstellung nicht möglich ist. Aus diesem Grunde werden bei praktischen Anwendungen der Katastrophentheorie meist nur die beiden einfachsten elementaren Katastrophentypen, nämlich die Faltenkatastrophe und die Spitzenkatastrophe behandelt. In der Abb. ist die Gleichgewichtsfläche der Spitzenkatastrophe dargestellt. »Katastrophen« ergeben sich in der Abb., wenn berücksichtigt wird, dass die langsamen Variablen zwar bisher als Parameter interpretiert wurden, aber sich doch langsam verändern. Es sei angenommen, dass die betrachteten drei Variablen ein allgemeines stabiles Gleichgewicht im Punkt A besitzen, d.h., x1, x2 und x3 ändern ihre Werte nicht mehr, falls sie einmal den Punkt A erreicht haben. Tritt eine kleine exogen bedingte Störung des Gleichgewichts auf, so werden die langsamen Variablen sich dem zugrundeliegenden dynamischen System entsprechend an den allgemeinen Gleichgewichtspunkt annähern (die Variable x1 nimmt wegen der genannten Annahmen immer ihren partiellen Gleichgewichtswert auf der Fläche M ein). Gibt es eine große Störung, dann sind in Abhängigkeit von der speziellen, unterstellten Form des dynamischen Systems zwei zeitliche Ablaufmuster möglich. a) Die exogene Störung versetzt das System in den Zustand F. Die Veränderungsgleichungen für x1 und x2 implizieren, dass der Entwicklungspfad über G zum allgemeinen Gleichgewicht A verläuft. Es findet eine Bewegung um die »Spitze« statt. b) Die exogene Störung versetzt das System in den Zustand C, und die Veränderungsgleichungen implizieren eine Bewegung in Richtung D. Bei D faltet sich die Gleichgewichtsfläche M jedoch zurück. Da die schnelle Variable xi sich bei der Spitzenkatastrophe nicht auf positiv ansteigenden Flächen niederlassen kann (weil eine sog. Bifurkationsmenge verlassen wird), muss ein partieller Gleichgewichtspunkt auf dem darüberliegenden, negativ ansteigenden Teil der Fläche liegen. Die Variable x1 muss von D zu E springen, d.h., es muss eine Katastrophe eintreten. Ist E erreicht, konvergieren x2 und x3 gegen den allgemeinen Gleichgewichtspunkt A. Eine entsprechende Betrachtung kann für (leicht abgeänderte) Varianten der Faltenkatastrophe durchgeführt werden. Es ist ferner möglich, Szenarien zu entwickeln, bei denen der allgemeine Gleichgewichtswert eines betrachteten Systems im positiv ansteigenden Bereich der Fläche M der Spitzenkatastrophe liegt; in diesem Fall können oszillierende Bewegungen mit Katastrophen jeweils beim Erreichen der Faltungen entstehen. Anwendungen der Katastrophentheorie in angewandten Disziplinen können als heuristische Betrachtungen der hinreichenden formalen Struktur interpretiert werden, die ein Modell aufweisen muß, um ein bestimmtes Phänomen beschreiben zu können. Es sei das Problem gestellt, unterschiedliche zeitliche Entwicklungsmuster wichtiger makroökonomischer Variablen wie - Sozialprodukt, Kapitalstock und Volksvermögen infolge von exogenen Störungen zu modellieren. Die Katastrophentheorie legt nahe, dieses Phänomen mit einer Modellstruktur zu erfassen, die der Spitzenkatastrophe entspricht. Die Variablen x1 und x2 seien als Sozialprodukt und Kapitalstock interpretiert, die Größe x3 sei eine Variable, die das Vermögen der Volkswirtschaft angibt. Eine Bewegung in Richtung der x3-Achse spiegele eine Verkleinerung des Vermögens wider. Bei einer starken, exogen verursachten Reduktion des Vermögens (möglicherweise infolge eines Börsenkrachs) befinde sich das System z.B. im Punkt F der Abb. der Spitzenkatastrophe. Es kann eine Bewegung um die Spitze eintreten, die wegen des langen Weges einen langen Zeitraum in Anspruch nimmt (Depression). Eine relativ schnelle Anpassung an das allgemeine Gleichgewicht mit einer abrupten Änderung des Sozialprodukts kann dann eintreten, wenn die exogene Störung das System in den Punkt C überführt. Die zeitliche Entwicklung kann über D und E zu A erfolgen (Rezession). Wie Hal R. VARIAN (1979) gezeigt hat, kann die für dieses zeitliche Muster erforderliche Modellstruktur z.B. bei bestimmten Konjunkturmodellen (Konjunkturtheorie) gegeben sein, in denen die Faltung durch entsprechend modellierte Investitionsfunktionen entsteht. Weitere katastrophentheoretische Ansätze finden sich in Betrachtungen von Stagflation, Reswitching in der Kapitaltheorie und in verschiedenen verhaltenstheoretischen Modellen. Wichtig ist, dass die von der Katastrophentheorie bereitgestellten formalen Werkzeuge aber nicht die Frage beantworten können, welches zeitliche Muster tatsächlich realisiert wird. Es ist hierzu die Entwicklung des ursprünglichen, anfangs erwähnten und konkreten dynamischen Systems zu kennen. Mit der Katastrophentheorie werden denkbare Ablaufmuster geschildert, denen ein konkretes System aber nicht zwangsläufig folgen muß. Literatur: Lorenz, H.-W. (1993). Ursprung, H.W. (1982). Varian, H.R. (1979). Zeeman, E.C. (1977)

Vorhergehender Fachbegriff: Katastrophenklausel | Nächster Fachbegriff: Katastrophenverschleiß

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : WVS | Administration Costs | Frei Haus

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer