Prognosetechnik

Gesamtheit der qualitativen und quantitativen Methoden, die zur Erarbeitung einer Prognose angewendet werden. Häufig versteht man darunter die numerischen Lösungsverfahren zur Auswertung quantitativer - Prognosemodelle.

liefert Methoden, um die Entwicklung einer ökonomischen Variablen y in Abhängigkeit insbes. von der Zeit (t, als unabhängiger Variable) vorherzusagen. Man unterscheidet dabei · univariable Methoden, die nur den Faktor Zeit als Einflußgröße betrachten; · multivariable Methoden, die weitere ökonomische Veränderliche neben der Zeit berücksichtigen. Grundlage der (hier allein diskutierten) univariablen Prognose sollte eine zuvor erstellte Zeitreihe sein. Diese versucht, Zusammenhänge zwischen einer Variablen und der Zeit aus Vergangenheitsbeobachtungen abzuleiten. Das Prinzip der Prognose beruht anschließend darauf, diese Zusammenhänge direkt oder in sinnvoll abgewandelter Form auf die Zukunft zu übertragen. Prinzipiell sind bei der Erstellung von Prognosen auch futuristische Methoden (ohne Ableitung aus Gesetzmäßigkeiten) oder heuristische (auf Erfahrung beruhende) Methoden möglich. Für die Ökonomik gebräuchlicher sind jedoch deterministische (ggf. mit stochastischem Rest) sowie stochastische Methoden. Eine zusätzliche Unterteilung der Prognosen erfolgt anhand ihrer Fristigkeit. Man unterscheidet kurzfristige (bis zu einem Jahr), mittel- und langfristige Prognosen. Welche Prognosemöglichkeiten im einzelnen zu wählen sind, hängt dabei zum einen von der Struktur des vorliegenden Datenmaterials ab (Möglichkeit einer Extrapolation in die Zukunft) und zum anderen von der gegebenen Zielsetzung (Prognosehorizont). a) Deterministische Methoden:
1. Als Methoden für kurzfristige Prognosen bieten sich zunächst (auch bei multivariabler Betrachtung) Methoden der Regressionsanalyse an, wobei die Zeit als unabhängige und die zu prognostizierende Größe als abhängige Variable betrachtet wird. Dabei wird ein funktionaler Zusammenhang aus der Vergangenheit auf die Zukunft übertragen. Die entsprechenden Parameter erhält man mittels der Methode der kleinsten Quadratsummen. Es ergeben sich somit Prognosewerte (y) der zu prognostizierenden Variablen in der Form eines Polynoms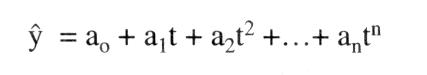
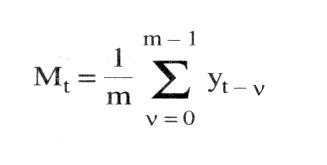Prognosetechnik

oder in Form exponentieller Gleichungen jeweils für den Prognosezeitpunkt t. Prinzipiell sind hier aber alle möglichen funktionalen Zusammenhänge denkbar. Eine weitere Methode beruht auf dem Prinzip der gleitenden Durchschnitte. Dabei wird der besonderen Struktur einer Zeitreihe, die sich nicht immer in Form einer einfachen Funktion darstellen läßt, Rechnung getragen. Eine Zeitreihe setzt sich i.d.R. aus einer glatten Komponente, die die langfristige Entwicklung (Trend) darstellt, und einer Saisonkomponente zusainmen, die regelmäßig wiederkehrende zyklische Schwankungen erfaßt. Daher benötigt man verschiedene Methoden, um diese beiden Phänomene zu erfassen, d.h., um die irregulären Schwankungen und die stochastischen Reste auszuschalten. Die Methode der gleitenden Durchschnitte ermittelt die Trendkomponente; daran anschließend erfolgt dann eine Schätzung der Saisonfigur. Um einen (linearen) Trend festzustellen, bildet man das arithmetische Mittel der letzten m Perioden
Prognosetechnik

sowie das arithmetische Mittel dieser gleitenden Durchschnitte, ebenfalls aus den letzten m Perioden (gleitende Durchschnitte
2. Ordnung),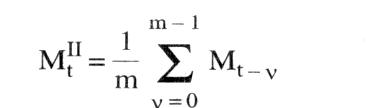
Prognosetechnik

Als Prognosewert für den Zeitpunkt t + i erhält man dann Besser eignet sich in diesem Zusammenhang die Methode der gewogenen gleitenden Durchschnitte. Dabei werden die in die Durchschnittsbildung eingehenden Werte entsprechend ihrer Bedeutung gewichtet, d.h., jüngere Daten gehen stärker in die Berechnung ein als ältere. Dies führt schließlich zum Prinzip des exponentiellen Glättens, das eine besondere Form der Methode der gewogenen gleitenden Durchschnitte darstellt. Dabei gehen die Vergangenheitswerte nicht mehr direkt in die Berechnung ein, sondern nur noch in Form eines Parameters a, des sog. Glättungsparameters, der entsprechend dem vorliegenden Datenmaterial geeignet gewählt werden muß. Dabei gilt 0 S a <_
1. Der Periode t zugeordnet wird als exponentiell geglätteter Mittelwert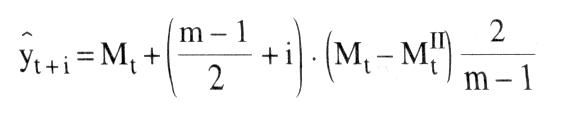
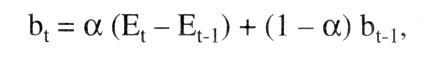Prognosetechnik

Für die Steigung der Trendgeraden ergibt sich
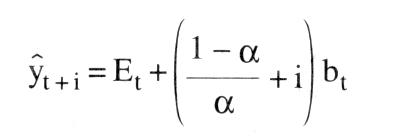Prognosetechnik

und somit folgt als Prognosewert für die Periode t + i
Prognosetechnik

Dabei stellt sich jedoch hier das Problem, geeignete Anfangswerte zu finden.
2. Als Methoden für mittel- und langfristige Prognosen kommen auch hier regressionsanalytische Verfahren in Betracht, solange kein Sättigungsniveau für die zu prognostizierende Variable beachtet werden muß. Insbes. bei Wachstumsprognosen (z.B. Neubedarfsprognosen) wird ein asymptotischer Verlauf gegen das Sättigungsniveau gegeben sein. Hier ist es sinnvoll und notwendig, Prognosen mit Hilfe der Klassen der logistischen bzw. GOMPERTZFunktinnen zn erctellen die diegem Verhalten Rechnung tragen. Dabei müssen die jeweils betrachteten Funktionen eine erste Ableitung ungleich Null, die sog. Wachstumsrate, besitzen. Die Stammfunktion der Klasse der logistischen Funktionen ist mit A. als Sättigungsniveau und G(t) = fg(t)dt mit g(t) als Beschreibung des Verhaltens (z.B. Kaufverhalten am Markt). Je nach Gestaltung von g(t) und damit von G(t) kommt man zu einem symmetrischen oder asymmetrischen Kurvenverlauf bei f. b) Stochastische Methoden: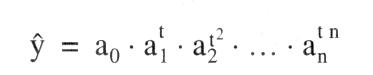
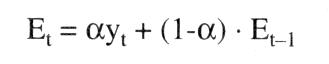Prognosetechnik

Das Grundprinzip von (hier allein diskutierten) Prognosen mittels MARKOV-Prozessen, geht davon aus, dass es sich bei der zu prognostizierenden Größe um eine Zufallsvariable handelt, die zum Zeitpunkt to = 0 einen gegebenen Vektor der Anfangswahrscheinlichkeiten (ao) ihrer Ausprägungen besitzt. Unter der Voraussetzung, dass die Anzahl der Ausprägungen endlich und zu jedem betrachteten Zeitpunkt gleich ist, ergibt sich der Vektor der Wahrscheinlichkeiten zum Zeitpunkt t =1 P bezeichnet hierbei die Matrix der Übergangswahrscheinlichkeiten vom Zeitpunkt t-1 zum Zeitpunkt t. Dieses Obergangsschema selbst ist keine Funktion der Zeit. Daher gilt auch
Prognosetechnik

Somit kann man für jeden Zeitpunkt t Wahrscheinlichkeiten prognostizieren Literatur: Lewandowski, R. (1980). Kendall, M., Stuart, A. (1976). Mertens, P. (1973)

Vorhergehender Fachbegriff: Prognosesysteme | Nächster Fachbegriff: Prognosetunktion

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Anzahlung | Lohnkostenkontrolle | Ungeld

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer