Stochastische Dominanz

Das Prinzip der stochastischen Dominanz wird bei Entscheidungssituationen unter Risiko ( Entscheidungsmodell) angewendet. Als Entscheidungsprinzip dient es dazu, unter mehreren Handlungsalternativen die jeweils unterlegenen Alternativen auszuschließen. Sind die Umweltsituationen bekannt, jedoch nicht deren Eintrittswahrscheinlichkeiten, so kann nur das allgemeingültige Dominanzprinzip eine Aussage über die dominierenden bzw. unterlegenen Handlungsalternativen machen. Sind dagegen außer den Umweltsituationen auch die Wahrscheinlichkeiten für deren Eintritt bekannt, so erlaubt das Prinzip der stochastischen Dominanz eine stärkere Reduzierung der unterlegenen Handlungsalternativen als das allgemeingültige Dominanzprinzip. Insoweit ist das Prinzip der stochastischen Dominanz dem Prinzip der allgemeingültigen Dominanz überlegen.

a) Stochastische Dominanz erster Ordnung (SDI): Eine ueivariate Zufallsvariable X mit der Verteilungsfunktion F(x) ist gegenüber einer Zufallsvariablen Y mit der Verteilung G(y) stochastisch dominant erster Ordnung, wenn für alle reellen Zahlen z gilt: F(z) <_ G(z) Für Entscheidungen bei Risiko und Unsicherheit impliziert dies, dass jeder Konsument mit einer NEUMANNMORGENSTERN-Nutzenfunktion u(z), u\'(z) > 0, eine riskante Anlage, deren Ertrag die Verteilung F(z) hat, einer Anlage mit Ertragsverteilung G(z) vorzieht. Es gilt nämlich für die Erwartungsnutzen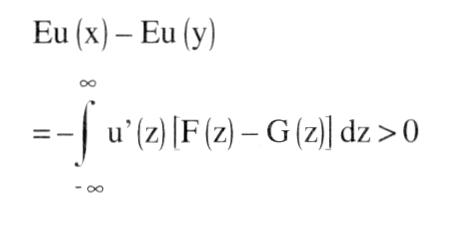
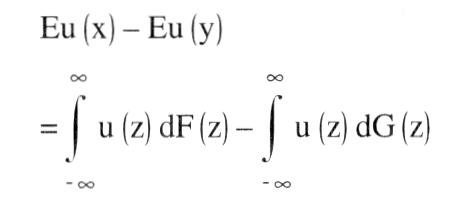stochastische Dominanz

bzw. nach partieller Integration
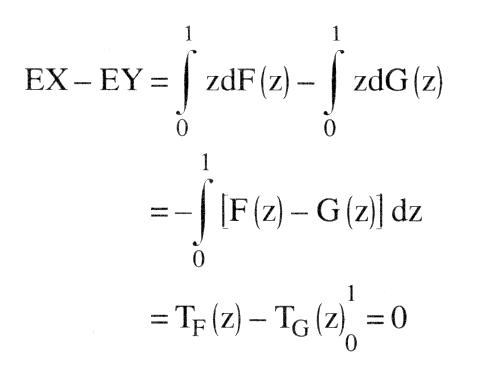stochastische Dominanz

Das Kriterium SD1 erlaubt somit eine Reihung riskanter Alternativen (z.B. Lotterien) unter minimalen Annahmen über die zugrundeliegenden Nutzenfunktionen. Ein wichtiges Anwendungsgebiet ist die Portfolio-Theorie. Andere Anwendungsmöglichkeiten sind komparativ-statische Analysen, in denen nicht eine deterministische exogene Größe, sondern eine Wahrscheinlichkeitsverteilung variiert wird. Ferner kann SD1 auch bei der Modellierung von Prinzipal-Agenten-Beziehungen verwendet werden, z.B. dann, wenn die (nicht direkt beobachtbare) Aktion des Agenten die Wahrscheinlichkeitsverteilung einer bestimmten Zielgröße beeinflußt. Zu beachten ist, dass SD1 immer nur partielle Ordnungen von Zufallsvariablen zuläßt, da sie nicht stets für beliebige Verteilungen erfüllt ist. b) Stochastische Dominanz zweiter Ordnung (SD2): Eine Zufallsvariable X mit Verteilung F(x) ist stochastisch dominant zweiter Ordnung gegenüber Y mit G(y), wenn für alle z gilt Die Ungleichung impliziert, dass jeder risikoscheue Konsument mit einer NEUMANN-MORGENSTERN-Nutzenfunktion u(z), wobei u\'(z) > 0 > u"(z), eine Lotterie mit der Verteilung F(x) gegenüber G(y) vorzieht. Es gilt Eu (x) — Eu (y)
stochastische Dominanz

wobei rechts vom Gleichheitszeichen zweimal partiell integriert wird, um den Ausdruck der ersten Zeile in den der dritten umzuformen. SD2 ist von Michael ROTHSCHILD und Joseph E. STIGLITZ (1970) verwendet worden, um die Riskantheit (RSR) zweier Verteilungen vergleichen zu können. Zu diesem Zweck wird zunächst angenommen, dass X und Y nur Werte aus dem Intervall [0, 1] annehmen. Ferner wird zusätzlich zu SD2 verlangt, dass gilt TF
(1) = TG
(1) d.h., dass die Erwartungswerte von X und Y gleich sind: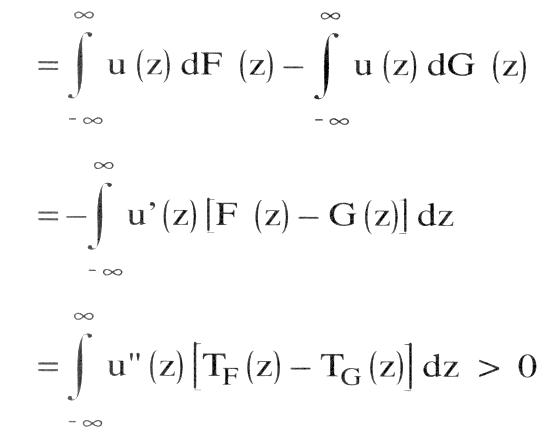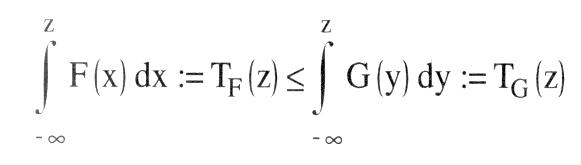
stochastische Dominanz

Eine Verteilung F(x) heißt weniger riskant als eine Verteilung G(y), wenn sowohl Bedingung SD2 als auch Bedingung TF(l) = TG
(1) erfüllt sind. Die intuitive Interpretation lautet, dass eine Lotterie, die einer anderen trotz gleicher erwarteter Auszahlung von allen risikoscheuen Konsumenten vorgezogen wird, ein geringeres Risiko aufweist. ROTHSCHILD und STIGLITZ haben auch gezeigt, dass RSR äquivalent zu anderen intuitiv ansprechenden Definitionen von Riskantheit sind. Addiert man z.B. zur Zufallsvariablen X eine Zufallsvariable S mit dem Erwartungswert ES = 0, so erfüllen X und X + S die Bedingungen RSR. Die Varianz einer Verteilung ist allerdings kein Riskantheitsindikator, der zur RSR äquivalent ist. Die ROTHSCHILD-STIGLITZ-Definition von Riskantheit kann auch für einen Vergleich von Einkommensverteilungen oder von Marktkonzentrationen herangezogen werden. »Große Riskantheit« ist (nach entsprechender Normierung) gleichbedeutend mit »gleichmäßigerer Verteilung« oder mit »geringerer Konzentration«. In die ökonomische Theorie kaum Eingang gefunden haben stochastische Dominanz dritter (oder höherer) Ordnung oder stochastische Dominanz von multivariaten Verteilungen. Bei diesen ist das Dominanzkriterium so restriktiv, dass es kaum intuitiv ansprechende Anwendungen gibt. Literatur: Whitmore, GA., Findley, M.C. (1978). Rothschild, M., Stiglitz, J.E. (1970)

Vorhergehender Fachbegriff: Stochastische Bedarfsermittlung | Nächster Fachbegriff: Stochastische Modelle

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Verbraucherforum | Produktionstyp | Kapazitätsauslastung

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer