| Empfehlungen |  |

Chi-Quadrat-Verteilung
|
theoretische Verteilung, die auf F. R. Helmert (1875) zurückgeht. Sie ist die Verteilung der Die Chi-Quadrat-Verteilung wird z.B. zur Bestimmung von Literatur: (x2) Entstammt eine zufällige Stichprobe (unabhängiger Beobachtungen) des Umf angs n mit der Varianz s2 einer normalverteilten (Normalverteilung) Grund gesamtheit mit der Varianz o2, dann gehorcht die durch x2 = (n1 JsVo2 definierte Zufallsvariable einer Chiquadratverteilung mit n1 Freiheitsgraden. Die Chiquadratverteilung ist eine stetige unsymmetrische Verteilung, deren Form ausschließlich durch die Anzahl der Freiheitsgrade geprägt wird. Sie nähert sich mit wachsender Zahl der Freiheitsgrade langsam einer Normalverteilung. Als sog. Prüfverteilung hat sie große Bedeutung in der Testtheorie (z. B. x2Anpassungstest, x2_Unabhängigkeitstest, x2_Homogenitätstest). Außerdem benötigt man sie zur Bestimmung von Konfidenzintervallen für Varianzen. Chlv) 04,. 5 10 15 20 v=l v=3 v=5 v=10 Dichtefunktionen der Chiquadratver teilung für v = 1, 3, 5 und 10 Freiheits grade Die Chi-Quadrat-Verteilung ist, wie die t- und F-Verteilung, ein „Abkömmling“ der Normalverteilung. Mit der F-Verteilung hat sie gemein, dass sie - als Quotient von Quadraten - bei 0 beginnt und nicht symmetrisch ist, mit der t-Verteilung, dass sie durch nur 1 Freiheitsgrad charakterisiert wird. (x2-Verteilung, HeImert-Pearson-Verteilung): Eine insbesondere für die Prüfung komplexer Hypothesen über die Streuung normalverteilter Zufallsgrößen z.B. in der Varianzanalyse oder für den Vergleich mehrerer Verteilungen (empirischer und theoretischer) geeignete stetige theoretische Prüfverteilung. Die Prüfung der Zufälligkeit der Differenzen zwischen den einzelnen Werten der Verteilungen erfolgt an der Summe der Quadrate der Differenzen (= x2). Sie hat die Dichtefunktion 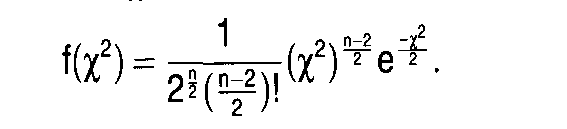 Der einzige Parameter dieser Verteilung ist n, das die Zahl der Freiheitsgrade bezeichnet. Die Verteilung nimmt nur positive Werte an. Mit wachsender Zahl der Freiheitsgrade nähert sie sich der Dichtefunktion einer Normalverteilung. Es handelt sich um eine eingipflige Verteilung, deren graphische Darstellung für kleine Freiheitsgrade schief ist und mit wachsender Zahl der Freiheitsgrade zunehmend flacher und symmetrischer wird. Für Chi-Quadrat-Verteilungen bestehen besondere Tabellen, die Zurückweisungsbereiche für verschiedene - Signifikanzniveaus unter Berücksichtigung der Freiheitsgrade und den ihnen zugeordneten Wahrscheinlichkeiten zeigen. 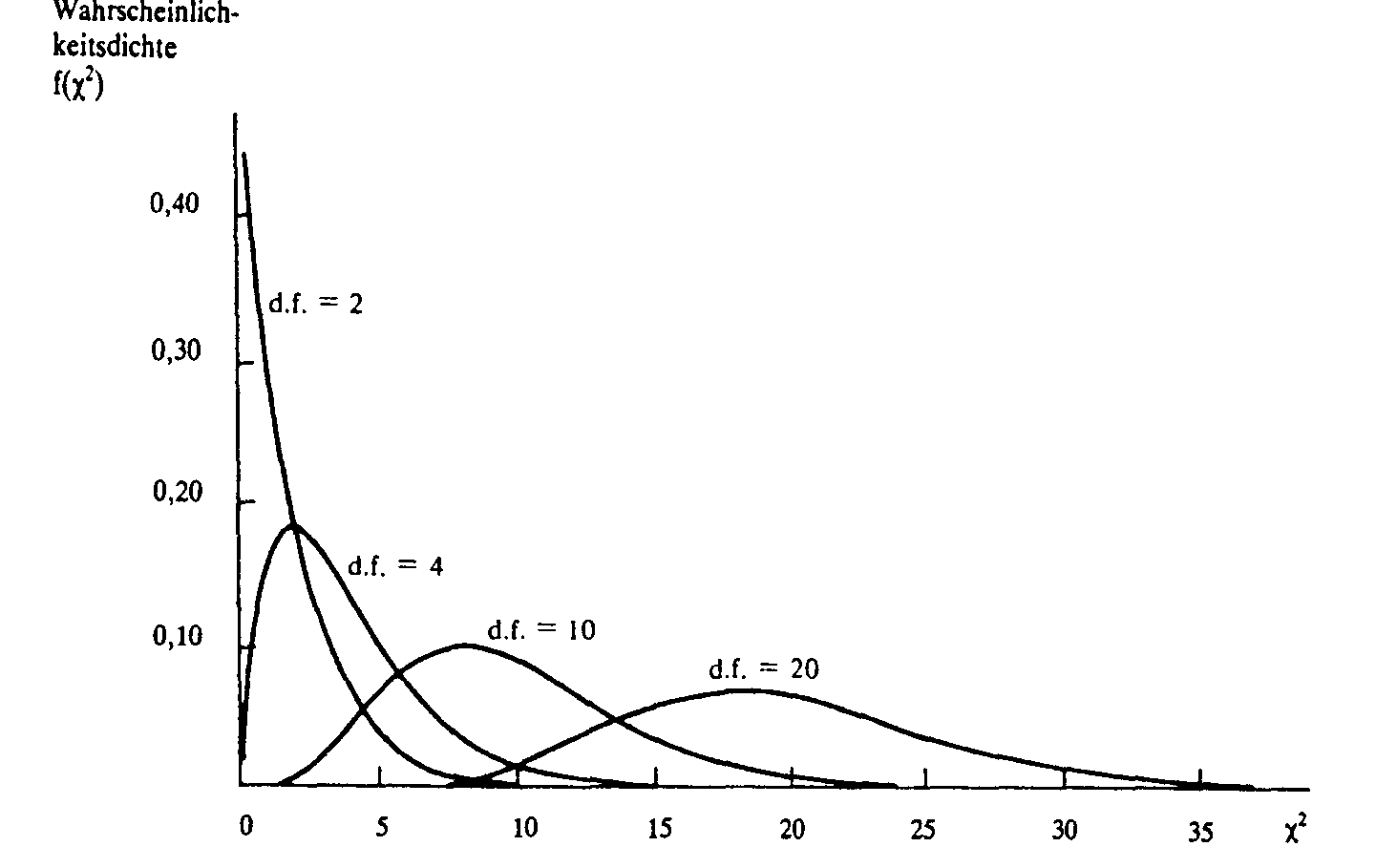 - Vorhergehender Fachbegriff: Chi-Quadrat-Test | Nächster Fachbegriff: Chicago Board of Options Exchange (CBOE) Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken |
|
Schreiben Sie sich in unseren kostenlosen Newsletter ein
Bleiben Sie auf dem Laufenden über Neuigkeiten und Aktualisierungen bei unserem Wirtschaftslexikon, indem Sie unseren monatlichen Newsletter empfangen. Garantiert keine Werbung. Jederzeit mit einem Klick abbestellbar.
Weitere Begriffe : Zollgesetz (ZG) | Bestandsänderung | unvollkommene Konkurrenz
|
Praxisnahe Definitionen Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar. |
Fachbegriffe der Volkswirtschaft Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre. |
Beliebte Artikel Bestimmte Erklärungen und Begriffsdefinitionen erfreuen sich bei unseren Lesern ganz besonderer Beliebtheit. Diese werden mehrmals pro Jahr aktualisiert. |
