| Empfehlungen |  |

Ertragsgesetz/Gesetz vom abnehmenden Ertragszuwachs
|
Das Ertragsgesetz (ausführlicher: Gesetz des abnehmenden Ertragszuwachses) stammt aus der Produktionstheorie, bezieht sich auf substituierbare Produktionsfaktoren (Substitutionsgüter) und lautet: Erhöht man die Einsatzmenge eines Faktors bei Konstanthaltung der übrigen Faktoren, so kann der Ertragszuwachs zunächst steigen, nach Überschreiten einer bestimmten Grenze muß der Ertragszuwachs abnehmen, nach Überschreiten einer zweiten Grenze muß er negativ werden. Problem: Das Ertragsgesetz gilt vor allem im landwirtschaftlichen Bereich. Die Übertragung auf die Industrie ist schwierig, unter anderem deshalb, weil hier limitationale Produktionsprozesse überwiegen. Beispiel: Wenn die Gesamtertragskurve den in der Abbildung gezeigten Verlauf hat, dann sind die Ertragszuwächse im Bereich I steigend, im Bereich II fallend und im Bereich III negativ. Das Ertragsgesetz, auch Gesetz vom abnehmenden Ertragszuwachs genannt, stellt das älteste produktionstheoretische Aussagensystem dar. Es wurde zuerst von dem französischen Physiokraten Anne Robert Jacques Turgot verbal für den Bereich der Landwirtschaft formuliert und danach von dem deutschen Klassiker Johann Heinrich von Thünen empirisch überprüft und theoretisch weiterentwickelt. Beim Ertragsgesetz, welches von Erich Gutenberg auch als Produktionsfunktion vom Typ A bezeichnet wird, wird davon ausgegangen, daß eine unmittelbare Beziehung zwischen dem Ertrag x und den Einsatzmengen ri, r2,..., r„ der Produktionsfaktoren Ri, R2,..., R. besteht: Dabei wird unterstellt, daß ein bestimmter Ertrag x mit Hilfe mehrerer unterschiedlicher Kombinationen von Faktoreinsatzmengen ri, r2,..., rn erstellt werden kann. Damit diese Bedingung erfüllt ist, müssen die Faktoreinsatzmengen in gewissen Grenzen untereinander ausgetauscht werden können, das heißt also, daß substitutionale Produktionsfaktoren unterstellt werden müssen. Das Ertragsgesetz enthält neben dem rein technischen Problem, welche Kombinationen der Faktoreinsatzmenge möglich sind, gleichzeitig auch das ökonomische Problem, welche Kombination bei gegebenen Preisen die wirtschaftlich günstigste ist. Die Frage, welche die optimale Kombination der Produktionsfaktoren ist, kann nur gelöst werden, wenn der produktive Beitrag jedes einzelnen Faktors am Gesamtertrag isoliert festgestellt werden kann. Dieses Zurechnungsproblem ist aber nur lösbar, wenn es gelingt, die Einsatzmengen eines Faktors zu variieren und die Einsatzmengen aller anderen Faktoren konstant zu halten. Dieser Tatbestand wird als partielle Faktorvariation bezeichnet. Werden zum Beispiel die Einsatzmengen des Faktors Ri variiert und die Einsatzmengen der Faktoren R2 bis R. konstant gehalten, dann kann die Produktionsfunktion auch wie folgt geschrieben werden: wobei r den variablen Faktor angibt. Eine Änderung des Ertrages ist dabei nur noch von einer Änderung der Einsatzmengen des variablen Faktors abhängig. Für die Gültigkeit des Ertragsgesetzes wird außerdem unterstellt, daß der variable Faktor beliebig teilbar ist, daß die Qualität der Faktoren unverändert bleibt, daß nur eine Produktart erzeugt wird, daß die Produktionstechnik nicht verändert wird und daß die Produktionsdauer vorgegeben ist. Die graphische Darstellung der Funktion x = f(r ergibt bei Gültigkeit des Ertragsgesetzes eine s-förmig verlaufende Gesamtertragskurve. Der Graph der Gesamtertragsfunktion zeigt die unmittelbare Beziehung zwischen dem Gesamtertrag x und der Variation der Einsatzmenge r des variablen Faktors bei Konstanz der übrigen Faktoren. Der Gesamtertrag x steigt zunächst erst langsam an, da die Einsatzmengen der konstanten Faktoren gegenüber der Einsatzmenge des variablen Faktors noch zu groß sind, um eine bessere Produktivität zu erreichen. Bei vermehrtem Einsatz des variablen Faktors wird das Wirkungsverhältnis zwischen den konstanten Faktoren und dem variablen Faktor immer günstiger, so daß der Gesamtertrag bis zum Wendepunkt progressiv ansteigt. In diesem ist, rein technisch gesehen, das günstigste Verhältnis zwischen den konstanten Faktoren und dem variablen Faktor erreicht. Danach überwiegt die Einsatzmenge des variablen Faktors, so daß der Gesamtertrag nur noch degressiv steigt, weil die Ertragszuwächse ständig abnehmen. Die Gesamtertragskurve erreicht schließlich ihr Maximum. Wird der variable Faktor weiter vermehrt, so sinkt der Gesamtertrag absolut. Der variable Faktor erbringt vom Maximum an keinen produktiven Beitrag, sondern wirkt sogar produktionszerstörend. Von den Prämissen des Ertragsgesetzes wird inbesondere die Annahme der Existenz von konstanten Prbduktionsfaktoren bestritten. Die Annahme der Konstanz bezieht sich nur auf die Konstanz des Bestandes, nicht aber auch auf die Konstanz der Leistungsabgabe. Unter der Annahme einer konstanten Intensität kann der erhöhte Einsatz nur einer Faktorart zu keiner Steigerung des Ertrages führen, wie es das Ertragsgesetz annimmt. Außerdem ist die Annahme substitutionaler Produktionsfaktoren für die industrielle Produktion, die vorwiegend durch limitationale Produktionsfaktoren gekennzeichnet ist, problematisch. Aus diesem Grunde ist nach Erich Gutenberg das Ertragsgesetz für die industrielle Produktion nicht als repräsentativ anzusehen. Gesetz vom abnehmenden Ertragszuwachs (Ertragsgesetz) (ertragsgesetzliche Produktionsfunktion) älteste wirtschaftswissenschaftliche Produktionsfunktion. Das Ertragsgesetz wurde bereits im 18. Jh. von Anne Robert Jacques Turgot und James Stewart im Hinblick auf die Erträge, insb. Ertragszuwächse, in der Landwirtschaft formuliert und später als Produktionshypothese für jede Art von Produktion verwendet. Ertragsgesetzliche Produktionsfunktionen bilden eine mehrfach unspezifi- zierte Klasse von Funktionen. Es gelten jedoch folgende (Definitions-) Merkmale: (1) Hinsichtlich ihrer mathematischen Eigenschaften gibt es bei der ertragsgesetzlichen Produktionsfunktion keine verbindlichen Regelungen. Von Bedeutung ist allerdings nur eine inputorientierte, skalarwertige Formulierung, wobei i.d.R. mindestens zweimalige stetige Differenzierbarkeit vorausgesetzt wird. (2) Den Kern des Ertragsgesetzes bildet eine Hypothese, die sich auf den Verlauf der partiellen Ertragsfunktionen bezieht. Eine partielle Ertragsfunktion (Produktionsfunktion, Faktorertragsfunktion) ergibt sich, wenn nur eine einzige Einsatzgütervariable bei Konstanz aller anderen variiert wird. Dabei wird ein zunächst überproportionaler, dann (mindestens in einem Punkt P) proportionaler und schliesslich unterproportionaler Verlauf (Produktionselastizität) bis zu einem Maximum M unterstellt. Anstelle dieses klassischen ertragsgesetzlichen Verlaufs wird bei neoklassischen (ertragsgesetzlichen) Funktionen die Hypothese auf die konkave (unterlineare) Zunahme des Gesamtertrags ab einer gewissen Einsatzmenge des variierten Faktors ("Wendepunkt" W) beschränkt (Gesetz vom abnehmenden Ertragszuwachs). Bei zwei variierenden Einsatzgütern lässt sich die Aussage des Ertragsgesetzes im Ertragsgebirge veranschaulichen. (3) Der Verlauf auf Skalen, d.h. die Entwicklung des Gesamtertrags bei Vermehrung des Inputs ohne Änderung seiner relativen Zusammensetzung von einem Ausgangspunkt an, ist bei ertragsgesetzlichen Funktionen im allgemeinen nicht festgelegt. So kann z. B. der ertragsgesetzliche Verlauf mit /konstanter Skalenelastizität (Homogenität) verknüpft werden. (4) Hinsichtlich weiterer Merkmale ist noch die Substituierbarkeit näher festgelegt. Mit abnehmenden Grenzerträgen z.B. ist nämlich nur eine (absolut) abnehmende Grenzrate der Substitution zwischen je zwei Einsatzgütern verträglich. Aus den Merkmalen des Ertragsgesetzes ergeben sich folgende Bedingungen für seine Anwendbarkeit: • Einstufige Einproduktfertigung (der Ertrag wird skalar gemessen, Zwischenprodukte werden nicht unterschieden). • Eines der Einsatzgüter oder eine Gruppe von ihnen wird mit konstanter Menge eingesetzt. • Das bzw. die anderen Einsatzgüter sind in ihrer Einsatzmenge teilbar und variierbar. Es liegt begrenzte (periphere) Substitutionalität der variierbaren Einsatzgüter vor. Wegen dieser engen Anwendungsbedingungen ist der Einsatzbereich des Ertragsgesetzes auf wenige Fälle hoch aggregierter volkswirtschaftlicher bzw. seltene Fälle betriebswirtschaftlicher Produktionen beschränkt. Ferner ist die empirische Geltung der Aussagen zumindest des klassischen Ertragsgesetzes umstritten* Dem Ertragsgesetz kommt daher allenfalls eine gewisse modellanalytische Bedeutung zu. Literatur: Küpper, H.-U., Das Ertragsgesetz, in: WiSt, 4. Jg. (1975), S. 131 ff. Schweitzer, MJKüp* per, H.-U., Produktions- und Kostentheorie der Unternehmung, Reinbek bei Hamburg 1974. gibt nach den landwirtschaftlichen Untersuchungen von Turgot (18. Jhdt.) die Abhängigkeit des Ernteertrags von variablen Produktionsfaktoren wie Saatgut, Düngemittel oder Arbeitseinsatz wieder. Es drückt einen charakteristischen Verlauf einer partiellen Faktorvariation aus, und zwar einen zunächst überproportional (progressiv), dann unterproportional (degressiv) und schliesslich ggf. rückläufig (regressiv) wachsenden Output. Dieser Verlauf lässt sich als Ausschnitt eines Produktionszusammenhangs mit einer linearen totalen Faktorvariation, nämlich eines Ertragsgebirges, verstehen. Siehe auch Produktions- und Kostentheorie. stammt aus der Produktionstheorie und beschreibt den Zusammenhang zwischen dem Produktionsergebnis und der Einsatzmenge eines Produktionsfaktors bei (hypothetisch oder tatsächlich) konstant gehaltenen Einsätzen der sonstigen Produktionsfaktoren. Man unterscheidet zwei Varianten. Nach dem klassischen Ertragsgesetz nimmt das Produktionsergebnis mit wachsendem Einsatz eines Faktors zunächst progressiv, dann degressiv zu und evtl. wieder ab. Es wurde von klassischen Ökonomen (Robert Jacques TURGOT, Johann Heinrich von THÜNEN) zunächst anhand von landwirtschaftlichen Produktionsprozessen untersucht. Man prüfte, wie der Ertrag einer gegebenen Bodenmenge mit dem Einsatz menschlicher Arbeit oder dem Einsatz der Düngemittel variiert. Nach dem neoklassischen Ertragsgesetz (auch das Gesetz vom abnehmenden Ertragszuwachs genannt) nimmt die Produktion von Anfang an degressiv zu. Man kann das neoklassische Ertragsgesetz als Spezialfall des klassischen ansehen. Es weist keinen Bereich progressiv zunehmenden und keinen Bereich absolut abnehmenden Produktionsergebnisses auf. Das klassische Ertragsgesetz läßt sich mittels der Ertragskurve darstellen. Eine Ertragskurve fur den Faktor 1 erhält man aus der – Produktionsfunktion Y = Y(X1, wenn man den - Output Y als Funktion von X1 für konstante sonstige Faktoreinsätze darstellt (Abb.) 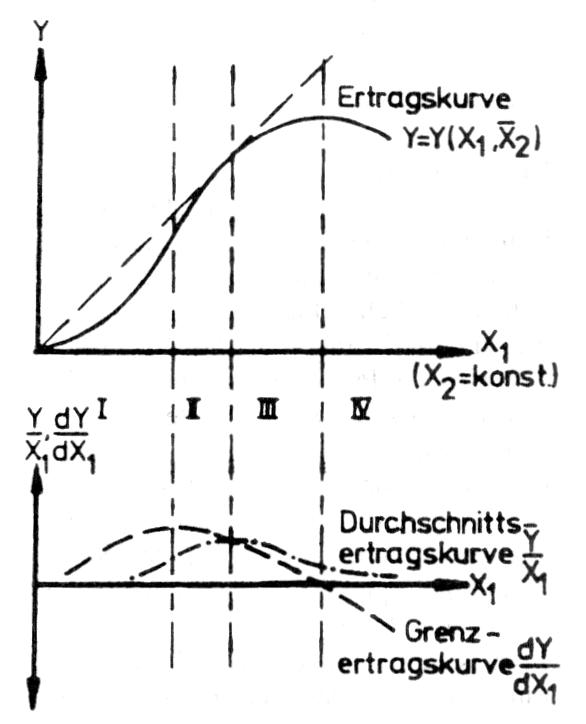 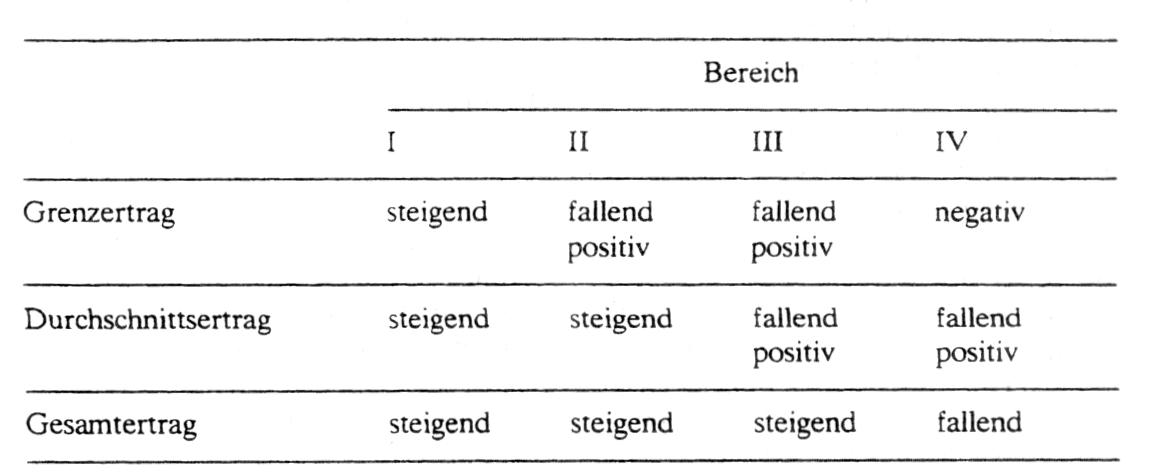 Unter Verwendung des Begriffs des Grenzertrages (der Grenzproduktivität), der als zusätzlicher Ertrag, bezogen auf eine infinitesimal kleine zusätzliche Faktoreinsatzmenge, definiert ist, gilt: Das klassische Ertragsgesetz impliziert bei steigendem Einsatz des variablen Faktors eine zunächst ansteigende, dann fallende und schließlich negative Grenzproduktivität des variablen Faktors. Der Durchschnittsertrag (die Durchschnittsproduktivität) des variablen Faktors nimmt ebenfalls zunächst zu und später ab. Je nach Zuordnung von Grenz-, Durchschnitts-und Gesamtertrag kann man vier Bereiche unterscheiden, die in obiger Tabelle wiedergegeben sind. Bei Gültigkeit des neoklassischen Ertragsgesetzes wären lediglich die Bereiche II und III relevant. Literatur: Ott, A.E. (1986) Unter Verwendung des Begriffs des Grenzertrages (der Grenzproduktivität), der als zusätzlicher Ertrag, bezogen auf eine infinitesimal kleine zusätzliche Faktoreinsatzmenge, definiert ist, gilt: Das klassische Ertragsgesetz impliziert bei steigendem Einsatz des variablen Faktors eine zunächst ansteigende, dann fallende und schließlich negative Grenzproduktivität des variablen Faktors. Der Durchschnittsertrag (die Durchschnittsproduktivität) des variablen Faktors nimmt ebenfalls zunächst zu und später ab. Je nach Zuordnung von Grenz-, Durchschnitts-und Gesamtertrag kann man vier Bereiche unterscheiden, die in obiger Tabelle wiedergegeben sind. Bei Gültigkeit des neoklassischen Ertragsgesetzes wären lediglich die Bereiche II und III relevant. Literatur: Ott, A.E. (1986)
Vorhergehender Fachbegriff: Ertragsgesetz | Nächster Fachbegriff: ertragsgesetzliche Kostenfunktionen Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken |
|
Schreiben Sie sich in unseren kostenlosen Newsletter ein
Bleiben Sie auf dem Laufenden über Neuigkeiten und Aktualisierungen bei unserem Wirtschaftslexikon, indem Sie unseren monatlichen Newsletter empfangen. Garantiert keine Werbung. Jederzeit mit einem Klick abbestellbar.
Weitere Begriffe : Girozentralen | Kundendatenbank | ZNR
|
Praxisnahe Definitionen Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar. |
Fachbegriffe der Volkswirtschaft Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre. |
Beliebte Artikel Bestimmte Erklärungen und Begriffsdefinitionen erfreuen sich bei unseren Lesern ganz besonderer Beliebtheit. Diese werden mehrmals pro Jahr aktualisiert. |
