Betriebswirtschaftliche Optimierung

Grundlagen der betriebswirtschaftlichen Optimierung

1. Charakterisierung Zur Entscheidungsunterstützung bei der Lösung komplexer Entscheidungs- und Planungsprobleme spielt die mathematische Optimierung in der Praxis seit Jahrzehnten eine wichtige Rolle. Das Entscheidungsproblem wird in einem mathematischen Modell (Optimierungsmodelle, mathematische) abgebildet, das dann in einem Computermodell implementiert wird und durch Optimierungssoftware gelöst wird. Für die betriebliche Praxis sind die Modellklassen Lineare Optimierungsmodelle (LP-Modelle, siehe Optimierungsmodelle, mathematische) und gemischt-ganzzahlige Optimierungsmodelle (IP-Modelle, siehe Optimierungsmodelle, mathematische) am wichtigsten, da es viele Anwendungen und hocheffiziente Standardsoftware gibt.
2. Anwendungsbereiche Praktische Anwendungen werden häufig im Rahmen eines Entscheidungsunterstützenden Systems realisiert, bei dem Datenhaltung, Modellgenerierung, Modelloptimierung und Ergebnisvisualisierung in einem anwenderfreundlichen Softwaresystem implementiert werden. Traditionell werden Optimierungsmodelle in der Mineralöl-, Petrochemischen- und Grundstoffindustrie eingesetzt. Anwendungen umfassen Einkaufs-, Produktions-, Mischungs-, Lagerhaltungs- und Transportprobleme. Zunehmend wird Optimierung auch bei strategischen und operativen Planungsproblemen in der Lieferkette eingesetzt. Linienfluggesellschaften setzen Optimierung für die Flug-, Rotations- und Dienstplanung ein. Auch bei der Optimierung (Auswahl und Platzierung) von Filialsortimenten erreicht man mit Optimierung signifikante Vorteile. Während sich auch sehr grosse LP-Modelle mit hunderttausenden von Variablen und Restriktionen in der Regel ohne Probleme lösen lassen, ist die Situation bei   IP-Modellen anders. Obwohl IP-Modelle formal eine grosse Ähnlichkeit zu LP-Modellen aufweisen, gehören sie (bis auf Ausnahmen) einer Modellklasse an, für die keine effizienten Algorithmen bekannt sind. Alle erfolgreichen Softwaresysteme zur Lösung von IP-Modellen basieren auf   Branch-and-Bound/CutAlgorithmen, bei denen sukzessive LP-Modelle gelöst werden, die sich nur durch verschärfte untere bzw. obere Schranken für einzelne ganzzahlige Variablen unterscheiden. Wesentliche Fortschritte bei der Lösung von IP-Modellen in der letzten Dekade basieren auf dem Konzept der strengen LPRelaxation im Rahmen des   IP-Preprocessing.
3. Gemischt-ganzzahlige Optimierungsmodelle Für die Lösung grosser gemischt-ganzzahliger Optimierungsmodelle sind folgende Einflussfaktoren von entscheidender Bedeutung:
1. eine mathematische Modellformulierung, die zu einer strengen LP-Relaxation führt;
2. ein effektives LP-Preprocessing, um redundante Modellteile zu entfernen und damit eine schnellere LP-Optimierung zu ermöglichen;
3. hocheffiziente LP-Optimierungskerne, da heutige Systeme viele   LP-Relaxationen lösen müssen;
4. ein effektives IP-Preprocessing, um eine möglichst strenge LP-Relaxation zu erzeugen. Das interne Modell kann dabei durch viele Cuts stark vergrössert werden;
5. Im   Branch-and-Bound/Cut-Algorithmus sind auch die Auswahlregeln für Branching-Variablen und die zu betrachtenden Teilmodelle (Knotenauswahl) sehr wichtig. Ein Benchmark Modell Oil mit ca. 5500 Restriktionen, 6000 Variablen und 35000 Nichtnullelementen zeigt am Beispiel der Optimierungssoftware MOPS, welche Fortschritte auf einem PC erreicht wurden. Die linke Tabelle zeigt die Lösungszeit für das Lösen des Anfangs-LPs des IP-Modells Oil. Die Laufzeit ist im Laufe der letzten 12 Jahre unter ein Prozent gesunken. In der rechten Tabelle wird das Modell Oil als IP-Modell gelöst. Dies beinhaltet die Lösung des Anfangs-LPs, das   IP-Preprocessing und die Lösung des modifizierten IP-Modells mit einem Branch-and-Cut-Algorithmus.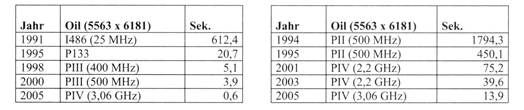
Betriebswirtschaftliche Optimierung

Die in den Tabellen dargestellte Laufzeitentwicklung basiert auf erheblichen Verbesserungen sowohl in der Hardware als auch in der Software. Der grösste Teil der Verbesserungen, insbesondere bei der Lösung von Oil als IP-Modell, stammt jedoch aus verbesserten Algorithmen, die auf jeder Systemplattform realisierbar sind.
4. Zusammenfassung und Ausblick Ständige Leistungssteigerungen bei Rechnern und Optimierungssoftware verbessern die Voraussetzungen für den praktischen Einsatz von Optimierungstechnologien. Vor allem bei gemischt-ganzzahliger Optimierung wurden in der letzten Dekade enorme Fortschritte bei den Algorithmen erzielt: Viele gemischt-ganzzahlige Modelle werden durch schnellere Algorithmen und Hardware mindestens um den Faktor 100 schneller gelöst. Allerdings werden Modelle aus praktischen Anwendungen immer grösser, so dass Optimierungssoftware immer wieder an Grenzen stösst. Weitere Fortschritte in der Lösung grosser und schwieriger IP-Modelle sind bei der Weiterentwicklung von Branch-and-Cut-Algorithmen sichtbar. Zwischenzeitlich sind Hochleistungs-PCs hinsichtlich Speicher und Rechenleistung prädestiniert für solche Anwendungen. In Verbindung mit komfortablen Benutzeroberflächen steigt damit Einsatzpotenzial und Akzeptanz der Applikationen. Hochentwickelte Modellierungssoftware erleichtert die Implementierung eines mathematischen Modells. Natürlich gibt es immer wieder Modelle, die nicht schnell genug oder gar nicht gelöst werden können. In der Praxis ist aber in den wenigsten Fällen ein Beweis der Optimalität einer Lösung erforderlich. Wenn nur eine „gute Lösung” bestimmt werden soll, so lässt sich die Laufzeit häufig drastisch verkürzen. Die Kombination aus Heuristik und Optimierungssoftware ermöglicht das schnelle Finden von ganzzahligen Lösungen mit dem Vorteil, Schranken für die Qualität einer Lösung zu erhalten. Hinweis Zu den angrenzenden Wissensgebieten bzw. zu Anwendungsbereichen siehe u.a. Analysemethoden, betriebswirtschaftliche, Beschaffungsmanagement, Beschaffungslogistik, Distributionslogistik, Entscheidung, betriebswirtschaftliche, Industriemanagement, Logistik, Nutzwertanalyse, Ökonometrie, Operation Research, Optimierungsmodelle, mathematische, Portfoliomanagement, Produktionsmanagement, Prozessmanagement, Statistik, Supply Chain Management, Wirtschaftsmathematik.

Literatur: Kallrath J. and J.M. Wilson, Business Optimisation using Mathematical Programming, Macmillan Press, 1997; Suhl, U.H. and H. Hilbert, A Branch-and-Cut-Algorithm for solving generalized Steiner Problems in Graphs, Networks 31
(4), 273-282, 1998; Suhl, U.H. and Suhl, L.M., Solving Airline Fleet Scheduling Problems with Mixed-Integer Programming, in „Operational Research in Industry”, Eds. T. Ciriani, S. Gliozzi, E.L. Johnson and R. Tadei, MacMillan Press Ltd., 135-156, 1999; Suhl, U.H., MOPS - Mathematical OPtimization System, OR News, 8, 11-16, 2000; Suhl, U.H., ITgestützte, operative Sortimentsplanung, in „IT-gestützte betriebswirtschaftliche Entscheidungsprozesse”, (Eds. B. Jahnke und F. Wall), Gabler, 175-194, 2001. Internetadressen: http://www.wiwiss.fu-berlin.de/suhl/; http://www-fp.mcs.anl.gov/otc/Guide/; http:// www.ilog.com/products/cplexi; http://www.dashoptimization.com/; http://www.mops-optimizer.com/

Vorhergehender Fachbegriff: Betriebswirtschaftliche Logistik | Nächster Fachbegriff: betriebswirtschaftliche Steuerlehre

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Girokonto | Franchise-Geber | Aktienanleihe

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer