Kostenfunktionen

(engl. cost functions) Kostenfunktionen zeigen die Veränderung der Kosten in Abhängigkeit von gewissen, meist betrieblichen Einflussgrößen. Kosten eines Betriebes oder eines Betriebsteils sind der bewertete, ordentliche Verzehr an Gütern und Dienstleistungen (Produktionsfaktoren, Verbrauchsfunktion) für die Leistungserstellung, die Leistungsverwertung und für die Aufrechterhaltung der Betriebsbereitschaft. Kosten variieren beispielsweise mit der Veränderung der Ausbringungsmenge (Ausbringung). Es wird dabei zwischen fixen Kosten (k Kosten, fixe) und variablen Kosten (a Kosten, variable) unterschieden. Die fixen Kosten K1 fallen überwiegend für die Aufrechterhaltung der Betriebsbereitschaft an. Die variablen Kosten Kv verändern sich bei Veränderung der Einflussgrößen, z. B. mit der Produktionsmenge x einer Produktart. Die Kostenfunktion lässt sich für diesen Fall in folgender Form ausdrücken: K(x) = K1+ Kv(x). Bei substitutionalen Produktionsfaktoren wird beispielsweise eine «ertragsgesetzliche Kostenfunktion» angenommen.

Bei dem Einsatz von limitationalen Produktionsfaktoren entstehen z. B. lineare Kostenfunktionen in Abhängigkeit von der Produktionsmenge x . Die Produktionsstufe folgt verschiedenen Mengenvorgaben x durch Anpassung der Produktionszeit: K(x) = Kf + k x mit k = variable Stückkosten = konstant. Wenn sowohl zeitliche als auch leistungsmäßige Anpassungen erfolgen (Produktionsfunktion vom Typ B), ergeben sich Kostenfunktionen mit linearen und nichtlinearen Teilfunktionen.

Bei weiteren Anpassungsmöglichkeiten (Anpassungsformen) an gewünschte Produktionsmengen durch Überstunden, Zuschaltung weiterer Maschinen (quantitative Anpassung) sowie Produktion in Schichten entstehen weitere Kostenfunktionen. Zur Erfassung der Informationsinhalte der Kostenverläufe werden auch die Verläufe der Grenzkosten und der Stückkosten (Durchschnittskosten, Einheitskosten) ermittelt.

Die Durchschnittskosten ergeben sich als Kosten pro Stück, indem die Kosten durch die Menge dividiert werden K = K/x. Es gibt totale Durchschnittskosten k und variable Durchschnittskosten = K)Jx sowie Durchschnittskosten k1aus fixen Kosten. Die totalen Durchschnittskosten setzen sich somit zusammen aus: k(x) =kv(x) + kf(x). Für die ertragsgesetzliche Kostenfunktion ergeben sich die gezeigten Grenzkosten und Stückkostenverläufe.

Im Minimum der Durchschnittskosten werden diese von den Grenzkosten geschnitten. Für den linearen Kostenverlauf, wie er gezeigt wird, sind die Funktionsverläufe dargestellt.

Wenn die Produktion sich aus mehreren Produktarten zusammensetzt, ergeben sich Kostenfunktionen in Abhängigkeit von mehreren Variablen x, i= 1,...,1. K = K(xf,x2,...,x1). Für die Erfassung der Steigungsmaße dieser Kostenfunktionen dienen die partiellen Grenzkosten, ermittelt als partielle erste Ableitungen der Kostenfunktion.

Kosten variieren auch in Abhängigkeit von anderen Einflussgrößen, so dass weitere Kostenfunktionen zu erwähnen sind. Kostenfunktionen in Abhängigkeit von der eingesetzten Menge r“ (n=1,...,N) der Produktionsfaktoren verlaufen linear, wenn die Faktorpreise q“ konstant sind:

Die Kontur gleicher Kosten bildet eine Gerade (Iso Kostengerade). Für mehr als zwei Faktorarten liegen die entsprechenden Mengenkombinationen auf einer Ebene oder Hyperebene. Für Faktorpreise q,,, die in Abhängigkeit von den Mengen r,, variieren, entstehen nichtlineare IsoKostenkonturen. Es gibt Transportkosten Funktionen, Lagerkosten Funktionen, Investitionskosten Funktionen und weitere Formen.

Der Zusammenhang zwischen der Menge der ausgebrachten Güter und den Kosten wird durch Kostenfunktionen hergestellt. Sie können entweder empirisch ermittelt werden, indem für eine Anzahl bekannter MengenKostenKombinationen mit Hilfe der Regressionsrechnung eine adäquate Funktion gesucht wird oder sie können deduktiv auf Grund von Prämissen über die zugrund eliegenden Produktionsfunktionen abgeleitet werden; dabei kann zwischen Kostenfunktionen auf der Basis der Gutenberg-Produktionsfunktion und Kostenfunktionen auf der Basis substitutionaler Produktionsfunktion unterschieden werden. Bei den Kostenfunktionen ist unabhängig von ihrer Herleitung hinsichtlich der Kostengrößen zu differenzieren: Kosten (pro Periode) K Durchschnittskosten k Grenzkosten K’ Diese drei Kostengrößen und ihre Funktionen stehen in folgendem Zusammenhang: Die Durchschnittskosten k ergeben sich aus den Kosten K durch Division durch die produzierte Menge x: x Die Grenzkosten K’ geben den Zu wachs der Kosten K an, der eintritt, wenn die produzierte Menge x um eine (infinitesimal kleine) Einheit er höht wird. Wenn die Kosten linear verlaufen, d. h. die variablen Stück kosten 1t» konstant sind, dann fallen die Durchschnittskosten stetig und die Grenzkosten sind gleich den va riablen Stückkosten k,. Wenn die Ko sten nicht linear verlaufen, sondern z. B. dem ertragsgesetzlichen Verlauf folgen, dann folgen die Durch schnittskosten einem parabelförmigen Verlauf, d. h. sie weisen ein relati ves Minimum auf und die Grenzko sten sind dann nicht gleich den varia blen Stückkosten und schneiden die Durchschnittskosten in deren Mini mum.

Die Kostenfunktion ist der Zusammenhang zwischen Ausbringungsmenge und Kosten; die Kostenfunktion gibt die Kosten an, die bei unterschiedlichen Ausbringungsmengen (Leistung, Produktion) mindestens anfallen.

Man charakterisiert unterschiedliche Kostenfunktionen mit Hilfe des Verlaufs der Gesamtkosten, variablen Kosten und Fixkosten, Stückkosten (Durchschnittskosten), variablen Stückkosten und Grenzkosten.

Problem:
(1) Im allgemeinen kann die Kostenfunktion nur für einen Kostenplatz oder eine Kostenstelle, nicht aber für den Gesamtbetrieb ermittelt werden (Ausnahme: Einprodukt-Unternehmung).

(2) Die Kostenfunktion gibt den Zusammenhang zwischen Ausbringungs menge und Kostenhöhe im Bereich von Nullproduktion bis Produktion an der Kapazitätsgrenze an. Tatsächlich verfügt man meist nur über Erfahrungswerte im Bereich der gegenwärtigen Istproduktion, so daß Verlaufsannahmen, die über den Istbereich hinausreichen, häufig spekulativen Charakter haben.

In der Praxis findet man meist die lineare Gesamtkostenfunktion mit degressiven Durchschnittskosten und konstanten Grenzkosten.

Funktion, die die Kostenhöhe in Abhängigkeit von den Kostenbestimmungsfaktoren angibt. Die Kostenfunktion kann aus der Produktionsfunktion unter Zugrundelegung einer Bewertung der verbrauchten Produktionsfaktoren mit Hilfe eines Kostenwertes abgeleitet werden.

Die Kostenfunktion gibt die funktionale Beziehung zwischen den Kosten und den Kosteneinflußgrößen an. Oft wird vereinfachend angenommen, daß die Kosten nur von der Beschäftigung abhängig seien, so daß gilt:

K = f(x)

Begriff | Symbol | Begriffsbestimmung | Dimension
-------------------------------------------------
Gesamtkosten | K | Gesamtkosten eines Betriebes für dieErstellung der betrieblichen Leistung in einer Periode | (EUR/Per)

-------------------------------------------------
variable Kosten | Kv | Kosten, die mit steigender Produktion steigen und mit fallender Prod. fallen. | (EUR/Per)

-------------------------------------------------
Fixkosten Kf Kosten der Betriebsbereitschaft, die bei einer Änderung der Ausbringungsmenge konstant bleiben (EUR/Per)

-------------------------------------------------

Stückkosten (Durchschnittskosten) k

Gesamtkosten
k = ----------------- =
Produktionsmenge

K
= --- EUR/Stück
x

Grenzkosten | K\' | Kostenänderung bei Änderung der Ausbringungsmenge um eine Einheit | EUR/Stück

Übers.: Kostenbegriffe zur Charakterisierung von Kostenfunktionen

bildet in der Kostentheorie die Abhängigkeit zwischen der Höhe der Kosten und den Ausprägungen der Kosteneinflussgrösse(n) ab. Kostenfunktionen stellen generelle Aussagen dar, die als nomologische Hypothesen die quantitativen Beziehungen zwischen der Kostenhöhe und ihren Einflussgrössen wiedergeben und dienen der Erkärung und Prognose von Kosten. Kostenfunktionen können nach mehreren Kriterien näher gekennzeichnet werden. Grundlegende Kriterien und die zugehörigen Erscheinungsformen sind in der Abbildung aufgeführt. Die Struktur einer Kostenfunktion ergibt sich unter Berücksichtigung der Mengen- und Wertkomponente von Kosten aus den Gesetzmässigkeiten für den Güterverbrauch und die Güterpreise. Der Güterverbrauch setzt sich aus dem Verzehr an Realgütern und an Nominalgütern zusammen. Der Verbrauch an Realgütern wird durch Produktionsfunktionen abgebildet, welche die gesetzmässigen Beziehungen zwischen dem Einsatz und dem Ausstoss an Realgütern wiedergeben. Funktionen über den Kapitalbedarf oder Kapitalverbrauch erfassen dagegen den Einsatz an Nominalgütern. Den dritten möglichen Baustein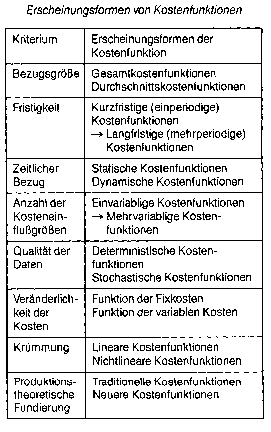

für Kostenfunktionen bilden neben Produktions- und Kapitalverbrauchsfunktionen Beschaffungspreis- bzw. Kostenwertfunktionen, welche die Gesetzmässigkeiten für die Wertkomponente von Kosten zum Ausdruck bringen. Nach der expliziten Berücksichtigung der Realgüterkomponente bei der Aufstellung von Kostenfunktionen kann zwischen traditionellen und neueren Kostenfunktionen unterschieden werden (vgl. Abb.). Für traditionelle Kostenfunktionen ist charakteristisch, dass die Analysen über die Kostenverläufe nicht auf Produktionsfunktionen aufbauen. Als einzige Kosteneinflussgrösse fungiert die Beschäftigung. Für verschiedene Kostenarten wird ein typisches Kostenverhalten bei Beschäftigungsänderungen postuliert, während aus den Annahmen über den Verlauf der ein zelnen Kostenarten für bestimmte Beschäftigungsintervalle mögliche Veränderungen der Gesamtkosten abgeleitet werden. Neuere Kostenfunktionen bauen ihre Kostenhypothesen auf Produktionsfunktionen auf. Ober den Zusammenhang von Einsatzgütern und Ausbringungsgütern sind unterschiedliche Gesetzmässigkeiten aufgestellt worden. Dementsprechend gibt es mehrere produktionstheoretisch fundierte Kostenfunktionen: • ertragsgesetzliche Kostenfunktionen, • Kostenfunktionen auf der Basis von Leon- tief-Produktionsfunktionen, • Kostenfunktionen auf der Basis der Produktionsfunktion vom Typ B (Erich Gutenberg), • Kostenfunktionen auf der Basis der Produktionsfunktion vom Typ C (Edmund Meinen), • Kostenfunktionen auf der Basis der Produktionsfunktion vom Typ D (Josef Kloock), • Kostenfunktionen auf der Basis der Produktionsfunktion vom Typ E (Hans-Ulrich Küpper). Gegenüber den traditionellen Kostenfunktionen kommt ihnen eine grössere Präzision der Aussagen über die Kosten Verläufe zu. Die Qualität ihrer Aussagen hängt von der Güte der verwendeten Produktionsfunktionen und der Berücksichtigung des Nominalgüterver- brauchs sowie der Kostenwerte ab. Literatur: Gutenberg, E., Grundlagen der Betriebswirtschaftslehre, Bd. 1: Die Produktion, 23. Aufl., Berlin u.a. 1979. Heinen, E., Betriebswirtschaftliche Kostenlehre, Kostentheorie und Kostenentscheidungen, 6. Aufl., Wiesbaden 1983. Küpper, H.-U., Interdependenzen zwischen Produktionstheorie und der Organisation des Produktionsprozesses, Berlin 1980.

Funktion, die die (Gesamt-)Kosten K in Abhängigkeit von der Ausbringungsmenge x eines Gutes ausdrückt: K = K(x). Die Kosten können dabei zerlegt werden in fixe und variable Kosten, wobei nur die variablen Kosten von x abhängen: K(x) = Kf Kv(x).

gibt die Kosten an, die bei Produktion alternativer Ausbringungsmengen eines Produktes mindestens enstehen. Sie sind von der Ausbringungsmenge Y und von den Preisen qi (j = 1,...,m) der eingesetzten Produktionsfaktoren abhängig: K=K(Y,qi............. q,,) Für konstante Faktorpreise kann man verkürzt schreiben K = K(Y). Die Beschaffenheit einer Kostenfunktion ergibt sich aus den Eigenschaften der zugrunde liegenden Produktionsfunktion. Die Kostenfunktion ist steigend in den Argumenten und linearhomogen (Homogenität) in den Faktorpreisen. Die Kosten in Abhängigkeit vom - Output verlaufen »spiegelbildlich« zu der Kurve, die die Abhängigkeit des Outputs vom totalen Faktoreinsatz zeigt: In Abb. 1 zeigt der Expansionspfad E die konstenminimierenden Faktormengenkombinationen, die Größe X das ProzeBniveau, Y(?) die Abhängigkeit des Outputs vom Prozeßniveau, wobei zunächst steigende und dann fallende Skalenerträge unterstellt werden. Der Strahl K(X) zeigt die Abhängigkeit der Kosten vom Prozeßniveau. Es resultiert die Kostenkurve K(Y). Sie verläuft spiegelbildlich zu Y(? ). Kurzfristig können einzelne Produktionsfaktoren häufig nicht optimal (kostenminimierend) an das jeweilige Produktionsniveau angepaßt werden. Ihr Einsatz ist fix, und sie verursachen Fixkosten. Die Kostenfunktion enthält dann die Mengen der im fixen Einsatz befindlichen Faktoren als zusätzliche Argumente. Kurzfristige Kostenkurven beruhen daher nur in eingeschränktem Mass auf dem Kostenminimierungsprinzip. Abb. 2 zeigt eine Kostenfunktion mit einem variablen Faktor für das klassische Ertragsgesetz.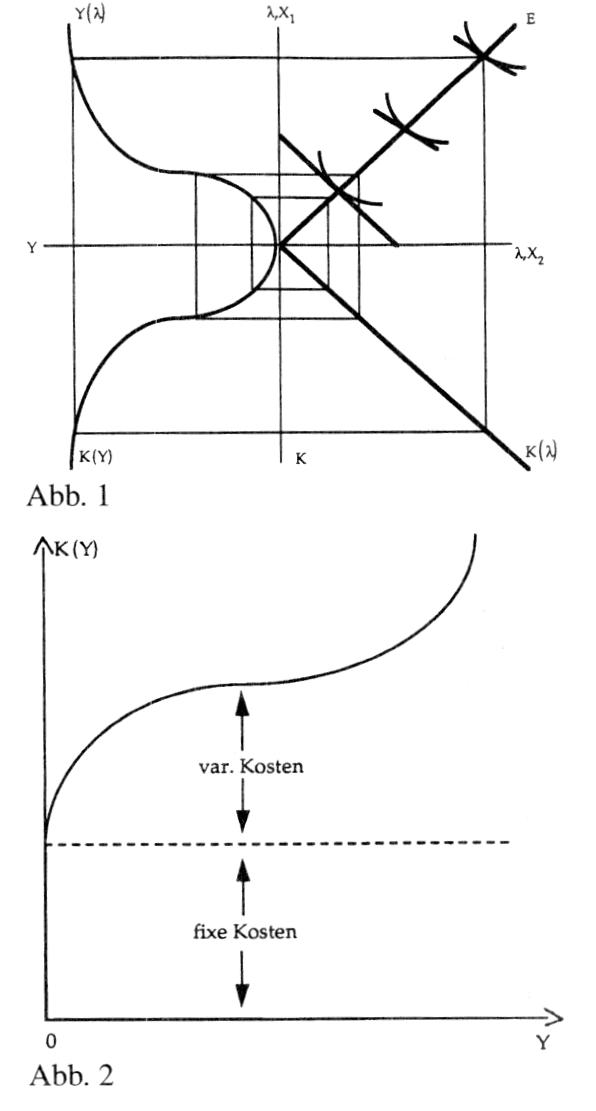

Literatur: Linde, R. (1992). Schumann, J. (1992)

Vorhergehender Fachbegriff: Kostenfunktion, psychophysische | Nächster Fachbegriff: Kostenfunktionen auf der Basis der Gutenberg-Produktionsfunktion

Diesen Artikel der Redaktion als fehlerhaft melden & zur Bearbeitung vormerken

Weitere Begriffe : Prüfungsverband | Wohnungsbauprämiengesetz | Start up

Praxisnahe Definitionen

Nutzen Sie die jeweilige Begriffserklärung bei Ihrer täglichen Arbeit. Jede Definition ist wesentlich umfangreicher angelegt als in einem gewöhnlichen Glossar.

Marketing

Definition

Konditionenpolitik

Fachbegriffe der Volkswirtschaft

Die Volkswirtschaftslehre stellt einen Grossteil der Fachtermini vor, die Sie in diesem Lexikon finden werden. Viele Begriffe aus der Finanzwelt stehen im Schnittbereich von Betriebswirtschafts- und Volkswirtschaftslehre.

Investitionsrechnungen

Marktversagen

Umsatzsteuer